
科目: 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=7,点E,F分别在边AD、BC上,且B、F关于过点E的直线对称,如果以CD为直径的圆与EF相切,那么AE= . 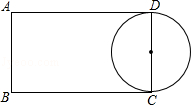
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,两个形状、大小完全相同的含有30゜和60゜的三角板如图放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.
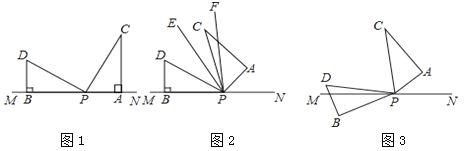
(1)试说明:∠DPC=90゜;
(2)如图2,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度,PF平分∠APD,PE平分∠CPD,求∠EPF;
(3)如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3゜/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2゜/秒,在两个三角板旋转过程中(PC转到与PM重合时,两三角板都停止转动),以下两个结论:①![]() 为定值;②∠BPN+∠CPD为定值,请选出正确的结论,并说明理由.
为定值;②∠BPN+∠CPD为定值,请选出正确的结论,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(-8,0),点A的坐标为(-6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,探究:当△OPA的面积为27时,求点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠AOB=90°,以O为顶点、OB为一边画∠BOC,然后再分别画出∠AOC与∠BOC的平分线OM、ON.
(1)在图1中,射线OC在∠AOB的内部.
①若锐角∠BOC=30°,则∠MON= °;
②若锐角∠BOC=n°,则∠MON= °.
(2)在图2中,射线OC在∠AOB的外部,且∠BOC为任意锐角,求∠MON的度数.
(3)在(2)中,“∠BOC为任意锐角”改为“∠BOC为任意钝角”,其余条件不变,(图3),求∠MON的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】(本题8分)如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两地相距720km,一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是120km/h,慢车的速度是80km/h,快车到达乙地后,停留了20min,由于有新的任务,于是立即按原速返回甲地.在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,这两次相遇时间间隔是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.
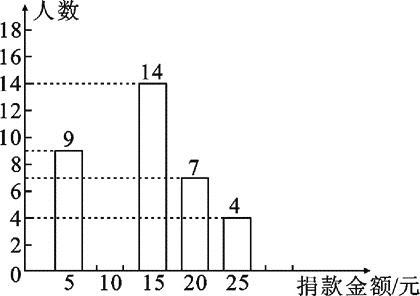
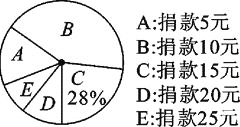
(1)本次共抽查学生________人,并将条形图补充完整;
(2)捐款金额的众数是________,平均数是________,中位数为________.
(3)在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到长方形AnBnCnDn(n>2),若ABn的长度为56,则n=_.
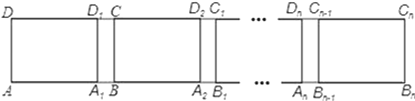
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= .(用含α与β的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com