
科目: 来源: 题型:
【题目】如图,在正方形 ABCD 中,点 E 是对角线 BD 上一动点,AE 的延长线交 CD 于点 F,交 BC 的延长线于点 G,M 是 FG 的中点.
(1)求证: ∠DAE=∠DCE;
(2)判断线段 CE 与 CM 的位置关系,并证明你的结论;
(3)当![]() ,并且
,并且![]() 恰好是等腰三角形时,求 DE 的长.
恰好是等腰三角形时,求 DE 的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】莫小贝在襄阳北街租了一家商铺专门销售各种旅游纪念品.本月初他在进货时发现:若购进甲种纪念品 3
件,乙种纪念品 2 件,需要 400 元,若购进甲种纪念品 4 件,乙种纪念品 5 件,需要 650 元. (1)求购进甲乙两种纪念品每件各需要多少元?
(2)若莫小贝决定购进这两种纪念品共 100 件,其中甲种纪念品的数量不少于 65 件.考虑到资金周转,用于购 买这些纪念品的资金不超过 9000 元,那么莫小贝共有几种进货方案?
(3)若每卖出一件甲种纪念品可获利润 20 元,一件乙种纪念品可获利润 35 元.在(2)的条件下,所购的 100 件 纪念品可以全部销售完,怎样进货才能使得获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要个小立方体,王亮所搭几何体的表面积为 . 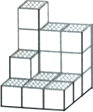
查看答案和解析>>
科目: 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P是∠AOB的边OB上的一点.
(1)过点M画OB的平行线MN;
(2)过点P画OA的垂线,垂足为H;
(3)过点P画OB的垂线,交OA于点C:
则线段PH的长度是点P到 的距离, 是点C到直线OB的距离,因为直线外一点到直线上各点连接的所有线段中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 .(用“<”号连接).
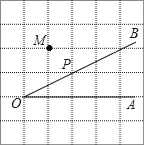
查看答案和解析>>
科目: 来源: 题型:
【题目】为了从甲乙两人中选拔一人参加初中数学竞赛,每个月对他们进行一次测试,如图绘出了两个人赛前 5 次测验成绩(每次测验成绩都是 5 的倍数).
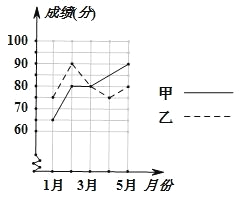
(1)分别求出甲乙两人 5 次测验成绩的平均数与方差;
(2)如果你是他们的辅导老师,应该选拔哪位学生参加这次竞赛,并简要说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某一广告墙PQ旁有两根直立的木杆AB和CD , 某一时刻在太阳光下,木杆CD的影子刚好不落在广告墙PQ上,
(1)你在图中画出此时的太阳光线CE及木杆AB的影子BF;
(2)若AB=6米,CD=3米 , CD到PQ的距离DQ的长为4米,求此时木杆AB的影长.
查看答案和解析>>
科目: 来源: 题型:
【题目】反比例函数 ![]() 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数 ![]() 的图象于点M , △AOM的面积为3.
的图象于点M , △AOM的面积为3.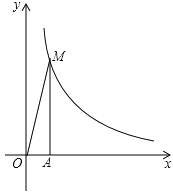
(1)求反比例函数的解析式;
(2)设点B的坐标为(t , 0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数 ![]() 的图象上,求t的值.
的图象上,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com