
科目: 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
6 | a | b | x | -2 | 1 | … |
(1)可求得x=______,第2016个格子中的数为______;
(2)判断:前m个格子中所填整数之和是否可能为2016?若能,求出m的值,若不可能,请说明理由;
(3)如果x,y为前3格子中的任意两个数,那么所有的|x-y|的和可以通过计算|6-a|+|a-6|+|a-b|+|b-a|+|6-b|+|b-6|得到.若x,y为前20格子中的任意两个数,则所有的|a-b|的和为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”
译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”
设井深为x尺,根据题意列方程,正确的是( )

A. 3(x+4)=4(x+1) B. 3x+4=4x+1
C. 3(x﹣4)=4(x﹣1) D. ![]()
查看答案和解析>>
科目: 来源: 题型:
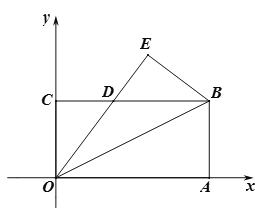
【题目】如图,矩形OABC的边OA,OC分别与坐标轴重合,并且点B的坐标为![]() .将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.
.将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.
(1)求证:△OBD为等腰三角形;
(2)求点E的坐标;
(3)坐标平面内是否存在一点F,使得以点B,E,F,O为顶点的四边形是平行四边形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),B→C( , ),C→ (+1, );
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出P的位置;

(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(4)若图中另有两个格点M、N,且M→A(3-a,b-4),M→N(5-a,b-2),则N→A应记为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】以下四个命题:
①对应角和面积都相等的两个三角形全等;
②“若x2﹣x=0,则x=0”的逆命题;
③若关于x、y的方程组 ![]() 有无数多组解,则a=b=1;
有无数多组解,则a=b=1;
④将多项式5xy+3y﹣2x2y因式分解,其结果为﹣y(2x+1)(x﹣3).
其中正确的命题的序号为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD ≌△ACE ;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.

查看答案和解析>>
科目: 来源: 题型:
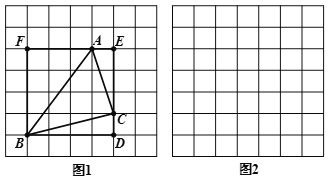
【题目】莫小贝在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C,A,她借助此图求出了△ABC 的面积.
(1)莫小贝所画的△ABC 的三边长分别是AB=_______,BC=______,AC=______;△ABC 的面积为________.
(2)已知△ABC 中,AB=![]() ,BC=
,BC=![]() ,AC=
,AC=![]() ,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.
,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com