
科目: 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,下列给出四个结论中,正确结论的个数是( )个
①c>0;
②若点B(﹣ ![]() ,y1)、C(﹣
,y1)、C(﹣ ![]() ,y2)为函数图象上的两点,则y1<y2;
,y2)为函数图象上的两点,则y1<y2;
③2a﹣b=0;
④ ![]() <0;
<0;
⑤4a﹣2b+c>0.
A.2
B.3
C.4
D.5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+2x﹣3与x轴交于A、B两点,且B(1,0)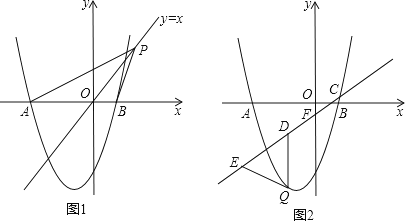
(1)求抛物线的解析式和点A的坐标;
(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;
(3)如图2,已知直线y= ![]() x﹣
x﹣ ![]() 分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将 ![]() 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.
沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC. 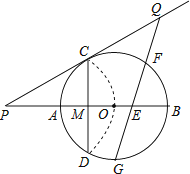
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为 ![]() 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交
的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 ![]() 于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:点D是△ABC所在平面内一点,连接AD、CD.
(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;
(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;
(3)如图3,在 (2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.

查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于y轴对称的△ABlCl;
(2)点P在x轴上,且点P到点B与点C的距离之和最小,直接写出点P的坐标为______.

查看答案和解析>>
科目: 来源: 题型:
【题目】荔枝是深圳的特色水果,小明的妈妈先购买了2千克桂味和3千克糯米糍,共花费90元;后又购买了1千克桂味和2千克糯米糍,共花费55元.(每次两种荔枝的售价都不变)
(1)求桂味和糯米糍的售价分别是每千克多少元;
(2)如果还需购买两种荔枝共12千克,要求糯米糍的数量不少于桂味数量的2倍,请设计一种购买方案,使所需总费用最低.
查看答案和解析>>
科目: 来源: 题型:
【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)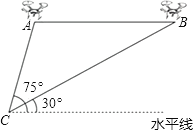
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
(1)如图,若点D为线段AC的中点,求证:AD=CE;
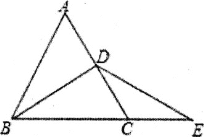
(2)如图,若点D为线段AC上任意一点,求证:AD=CE.

查看答案和解析>>
科目: 来源: 题型:
【题目】小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com