
科目: 来源: 题型:
【题目】四个规模不同的滑梯A , B , C , D , 它们的滑板长(平直的)分别为300m , 250m , 200m , 200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法( )
A.A的最高
B.B的最高
C.C的最高
D.D的最高
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米 . 求放水后水面上升的高度是( )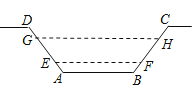
A.0.55
B.0.8
C.0.6
D.0.75
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD为∠BAC的平分线,添加下列条件后,不能证明△ABD≌△ACD的是( )

A. ∠B=∠C B. ∠BDA=∠CDA C. BD=CD D. AB=AC
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3 ![]() 米,坡顶有旗杆BC , 旗杆顶端B点与A点有一条彩带相连 . 若AB=10米,则旗杆BC的高度为( )
米,坡顶有旗杆BC , 旗杆顶端B点与A点有一条彩带相连 . 若AB=10米,则旗杆BC的高度为( )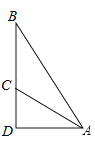
A.5米
B.6米
C.8米
D.(3+ ![]() )米
)米
查看答案和解析>>
科目: 来源: 题型:
【题目】在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)( )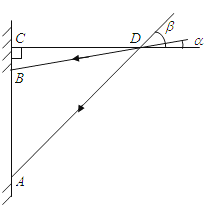
A.1.2米
B.1.5米
C.1.9米
D.2.5米
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC , 支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( ) (栏杆宽度,汽车反光镜忽略不计)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75 . 车辆尺寸:长×宽×高)
A.宝马Z4(4200mm×1800mm×1360mm)
B.奇瑞QQ(4000mm×1600mm×1520mm)
C.大众朗逸(4600mm×1700mm×1400mm)
D.奥迪A4(4700mm×1800mm×1400mm)
查看答案和解析>>
科目: 来源: 题型:
【题目】数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A.B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E , 再从E沿着垂直于AE的方向走到F , C为AE上一点,其中3位同学分别测得三组数据:①AC , ∠ACB;②EF.DE.AD;③CD , ∠ACB , ∠ADB.其中能根据所测数据求得A.B两树距离的有( )
A.0组
B.一组
C.二组
D.三组
查看答案和解析>>
科目: 来源: 题型:
【题目】数学活动课上,小敏.小颖分别画了△ABC和△DEF , 尺寸如图 . 如果两个三角形的面积分别记作S△ABC.S△DEF , 那么它们的大小关系是( )
A.S△ABC>S△DEF
B.S△ABC<S△DEF
C.S△ABC=S△DEF
D.不能确定
查看答案和解析>>
科目: 来源: 题型:
【题目】问题背景
在△ABC中,AB,BC,AC的长分别为![]() ,
,![]() ,
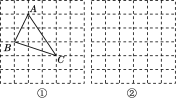
,![]() ,求这个三角形的面积.晓辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点三角形ABC(即△ABC的三个顶点都在小正方形的顶点处),如图①所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.晓辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点三角形ABC(即△ABC的三个顶点都在小正方形的顶点处),如图①所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你直接写出△ABC的面积:________.
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC的三边长分别为![]() a,2
a,2![]() a,
a,![]() a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
探索创新
(3)若△ABC的三边长分别为![]() ,
,![]() ,2
,2![]() (m>0,n>0,且m≠n),试运用构图法(自己重新设计一个符合结构特征的网格)求出这个三角形的面积.
(m>0,n>0,且m≠n),试运用构图法(自己重新设计一个符合结构特征的网格)求出这个三角形的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某沿海城市A接到台风警报,在该城市正南方向260 km的B处有一台风中心,沿BC方向以15 km/h的速度向C移动,已知城市A到BC的距离AD=100 km,那么台风中心经过多长时间从B点移动到D点?如果在距台风中心30 km的圆形区域内都将受到台风的影响,正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com