
科目: 来源: 题型:
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | 9.5 |
(1)完成表中填空①;②;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为 ![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,A,B,C三点的坐标为( ![]() ,0)、(3
,0)、(3 ![]() ,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10cm,BC=12cm,点P从点C出发,在线段CB上以每秒1cm的速度向点B匀速运动.与此同时,点M从点B出发,在线段BA上以每秒lcm的速度向点A匀速运动.过点P作PN⊥BC,交AC点N,连接MP,MN.当点P到达BC中点时,点P与M同时停止运动.设运动时间为t秒(t>0).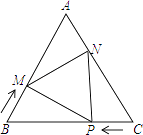
(1)当t为何值时,PM⊥AB.
(2)设△PMN的面积为y(cm2),求出y与x之间的函致关系式.
(3)是否存在某一时刻t,使S△PMN:S△ABC=1:5?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题提出:如图(1),在边长为a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求S正方形MNPQ . 问题探究:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图(2)).
(1)若将上述四个等腰三角形拼成一个新的正方形(无缝隙,不重叠),则新正方形的边长为;这个新正方形与原正方形ABCD的面积有何关系;(填“>”,“=”“或<”);通过上述的分析,可以发现S正方形MNPQ与S△FSB之间的关系是:
(2)问题解决:求S正方形MNPQ .
(3)拓展应用:如图(3),在等边△ABC各边上分别截取AD=BE=CF=1,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△PQR,求S△PQR . (请仿照上述探究的方法,在图3的基础上,先画出图形,再解决问题).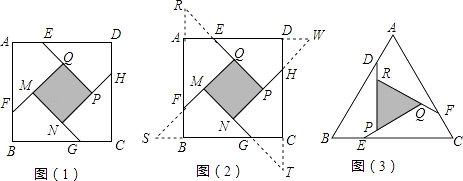
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,ABCD的两条对角线相交于点O,E是BO的中点.过点B作AC的平行线BF,交CE的延长线于点F,连接AF. 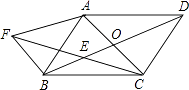
(1)求证:△FBE≌△COE;
(2)将ABCD添加一个条件,使四边形AFBO是菱形,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,隧道的截面由抛物线和长方形构成.长方形的长为12m,宽为5m,抛物线的最高点C离路面AA1的距离为8m,建立如图所示的直角坐标系. 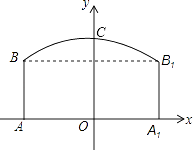
(1)求该抛物线的函数表达式,并求出自变量x的取值范围;
(2)一大型货运汽车装载大型设备后高为6m,宽为4m.如果该隧道内设双向行车道,那么这辆货车能否安全通过?
查看答案和解析>>
科目: 来源: 题型:
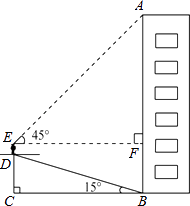
【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m) (参考数据:sin15°= ![]() ,cos15°=
,cos15°= ![]() ,tan15°=
,tan15°= ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com