【题目】如图1，在四边形ABCD中，AD∥BC，∠B=∠C=60°，P、Q同时从B出发，以每秒1单位长度分别沿B﹣A﹣D﹣C和B﹣C﹣D方向运动至相遇时停止，设运动时间为t（秒），△BPQ的面积为S（平方单位），S与t的函数图象如图2所示，则下列结论错误的个数（ ）
①当t=4秒时，S=4 ②AD=4
③当4≤t≤8时，S=2 t ④当t=9秒时，BP平分四边形ABCD的面积．

A.1个
B.2个
C.3个
D.4个

【题目】如图，在边长为1的菱形ABCD中，∠DAB=60°，连接对角线AC，以AC为边作第二个ACC1D1 ， 使∠D1AC=60°；连接AC1 ， 再以AC1为边作第三个菱形AC1C2D2 ， 使∠D2AC1=60°；…，按此规律所作的第2017个菱形的边长为（ ）
A.（ ）2016
B.（ ）2016
C.22017
D.（ ）2017

【题目】如图，在矩形ABCD中，AB=3，BC=5，在CD上任取一点E，连接BE，将△BCE沿BE折叠，使点C恰好落在AD边上的点F处，则CE的长为（ ）
A.2
B.
C.1
D.

【题目】如图1，抛物线y=﹣x2+bx+c经过A（﹣1，0），B（4，0）两点，与y轴相交于点C，连结BC，点P为抛物线上一动点，过点P作x轴的垂线l，交直线BC于点G，交x轴于点E．

（1）求抛物线的表达式；
（2）当P位于y轴右边的抛物线上运动时，过点C作CF⊥直线l，F为垂足，当点P运动到何处时，以P，C，F为顶点的三角形与△OBC相似？并求出此时点P的坐标；
（3）如图2，当点P在位于直线BC上方的抛物线上运动时，连结PC，PB，请问△PBC的面积S能否取得最大值？若能，请求出最大面积S，并求出此时点P的坐标，若不能，请说明理由．

【题目】请阅读下列材料：
问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB= ，PC=1、求∠BPC度数的大小和等边三角形ABC的边长．
李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2），连接PP′，可得△P′PC是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证），所以∠AP′B=150°，而∠BPC=∠AP′B=150°，进而求出等边△ABC的边长为 ，问题得到解决．
请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA= ，BP= ，PC=1．求∠BPC度数的大小和正方形ABCD的边长．

【题目】某超市销售甲、乙两种糖果，购买3千克甲种糖果和1千克乙种糖果共需44元，购买1千克甲种糖果和2千克乙种糖果共需38元．
（1）求甲、乙两种糖果的价格；
（2）若购买甲、乙两种糖果共20千克，且总价不超过240元，问甲种糖果最少购买多少千克？

【题目】在ABCD中，过点D作DE⊥AB于点E，点F在边CD上，DF=BE，连接AF，BF．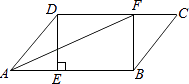
（1）求证：四边形BFDE是矩形；
（2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB．

【题目】某兴趣小组借助无人飞机航拍校园．如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°．已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．（结果保留根号）

【题目】平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起，如图，则∠3+∠1﹣∠2= ．

【题目】宽与长的比是 （约0.618）的矩形叫做黄金矩形，黄金矩形蕴藏着丰富的美学价值，给我们以协调和匀称的美感．我们可以用这样的方法画出黄金矩形：作正方形ABCD，分别取AD、BC的中点E、F，连接EF：以点F为圆心，以FD为半径画弧，交BC的延长线于点G；作GH⊥AD，交AD的延长线于点H，则图中下列矩形是黄金矩形的是（ ）
A.矩形ABFE
B.矩形EFCD
C.矩形EFGH
D.矩形DCGH