
科目: 来源: 题型:
【题目】如图,△ABC中,将△ABC绕点A顺时针旋转40°后,得到△AB′C′,且C′在边BC上,则∠AC′C的度数为( ) 
A.50°
B.60°
C.70°
D.80°
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:正方形ABCD的边长为4,点E为BC的中点,点P为AB上一动点,沿PE翻折△BPE得到△FPE,直线PF交CD边于点Q,交直线AD于点G,联接EQ.
(1)如图,当BP=1.5时,求CQ的长;
(2)如图,当点G在射线AD上时,BP=x,DG=y,求y关于x的函数关系式,并写出x的取值范围;
(3)延长EF交直线AD于点H,若△CQE与△FHG相似,求BP的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过点A(4,0),C(0,﹣4),另有一点B(﹣2,0).
(1)求一次函数解析式;
(2)联结BC,点P是反比例函数y= ![]() 的第一象限图象上一点,过点P作y轴的垂线PQ,垂足为Q.如果△QPO与△BCO相似,求P点坐标;
的第一象限图象上一点,过点P作y轴的垂线PQ,垂足为Q.如果△QPO与△BCO相似,求P点坐标;
(3)联结AC,求∠ACB的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点E是四边形ABCD的对角线BD上的一点,∠BAE=∠CBD=∠DAC. 
(1)求证:DEAB=BCAE;
(2)求证:∠AED+∠ADC=180°.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AD∥BC,点E在边AD上,CE与BD相交于点F,AD=4,AB=5,BC=BD=6,DE=3. 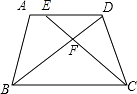
(1)求证:△DFE∽△DAB;
(2)求线段CF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F. 
(1)如果AB=6,BC=8,DF=21,求DE的长;
(2)如果DE:DF=2:5,AD=9,CF=14,求BE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AD∥BC,AD= ![]() BC,点M是边BC的中点,
BC,点M是边BC的中点, ![]() =
= ![]() ,
, ![]() =
= ![]() .
. 
(1)填空: ![]() = ,
= , ![]() = . (结果用
= . (结果用 ![]() 、
、 ![]() 表示).
表示).
(2)直接在图中画出向量3 ![]() +
+ ![]() .(不要求写作法,但要指出图中表示结论的向量)
.(不要求写作法,但要指出图中表示结论的向量)
查看答案和解析>>
科目: 来源: 题型:
【题目】将ABCD(如图)绕点A旋转后,点D落在边AB上的点D′,点C落到C′,且点C′、B、C在一直线上.如果AB=13,AD=3,那么∠A的余弦值为 . 
查看答案和解析>>
科目: 来源: 题型:
【题目】新定义:我们把两条中线互相垂直的三角形称为“中垂三角形”.如图所示,△ABC中,AF、BE是中线,且AF⊥BE,垂足为P,像△ABC这样的三角形称为“中垂三角形”,如果∠ABE=30°,AB=4,那么此时AC的长为 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com