
科目: 来源: 题型:
【题目】随着互联网、移动终端的迅速发展,数字化阅读越来越普及,公交上的“低头族”越来越多.某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(如图1),并将调查结果绘制成图2和图3所示的统计图(均不完整).
请根据统计图中提供的信息,解答下列问题:
(1)求出本次接受调查的总人数,并将条形统计图补充完整;
(2)表示观点B的扇形的圆心角度数为度;
(3)若嘉善人口总数约为60万,请根据图中信息,估计嘉善市民认同观点D的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4). 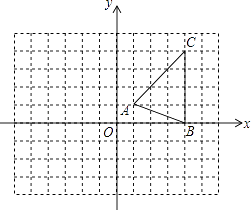
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2 .
(2)求点C1在旋转过程中所经过的路径长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,对正方形纸片ABCD进行如下操作:
(I)过点D任作一条直线与BC边相交于点E1(如图①),记∠CDE1=a1;
(II)作∠ADE1的平分线交AB边于点E2(如图②),记∠ADE2=a2;
(III)作∠CDE2的平分线交BC边于点E3(如图③),记∠CDE3=a3;
按此作法从操作(2)起重复以上步骤,得到a1 , a2 , …,an , …,现有如下结论:
①当a1=10°时,a2=40°;
②2a4+a3=90°;
③当a5=30°时,△CDE9≌△ADE10;
④当a1=45°时,BE2= ![]() AE2 .
AE2 .
其中正确的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角坐标系xOy中,A(﹣4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( ) 
A.(1, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,2
,2 ![]() )
)
D.( ![]() ,2
,2 ![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=ax2+bx+c的图象向左平移5个单位或向右平移1个单位后都会经过原点,则此抛物线的对称轴与x轴的交点的横坐标是( )
A.2
B.﹣2
C.3
D.﹣3
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,点A,B分别是二次函数y=2x2的图象上的两个点,A、B的横坐标分别为a,b(a<0,b>0),点P(0,t)是抛物线对称轴上的任意一点.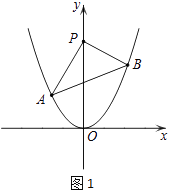
(1)当a+b=0时,探究是否存在t,使得△PAB是以AB为底的等腰三角形?若存在,请直接写出t、a、b的其中一组值;若不存在,请说明理由;
(2)当a+b≠0时,探究是否存在t,使得△PAB是以AB为底的等腰三角形?若存在,请写出t的取值范围,并用含t的代数式表示a2+b2的值;若不存在,请说明理由;
(3)如图2作边长为4的正方形ACDE(A、C、D、E按逆时针排列),使得AC∥x轴,若边CD与二次函数的图象总有交点,求a的取值范围.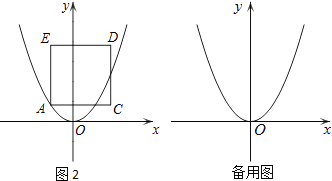
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,新定义:直线l1、l、l2 , 相交于点O,长为m的线段AB在直线l2上,点P是直线l1上一点,点Q是直线l上一点.若∠AQB=2∠APB,则我们称点P是点Q的伴侣点;
(1)如图1,直线l2、l的夹角为30°,线段AB在点O右侧,且OA=1,m=2,若要使得∠APB=45°且满足点P是点Q的伴侣点,则OQ= 
(2)如图2,若直线l1、l2的夹角为60°,且m=3,若要使得∠APB=30°,线段AB在直线l2上左右移动.
①当OA的长为多少时,符合条件的伴侣点P有且只有一个?请说明理由;
②是否存在符合条件的伴侣点P有三个的情况?若存在,请直接写出OA长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为进一步缓解城市交通压力,义乌市政府推出公共自行车,公共自行车在任何一个网店都能实现通租通还,某校学生小明统计了周六校门口停车网点各时段的借、还自行车数,以及停车点整点时刻的自行车总数(称为存量)情况,表格中x=1时的y的值表示8:00点时的存量,x=2时的y值表示9:00点时的存量…以此类推,他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
时段 | x | 还车数 | 借车数 | 存量y |
7:00﹣8:00 | 1 | 7 | 5 | 15 |
8:00﹣9:00 | 2 | 8 | 7 | n |
… | … | … | … | … |
根据所给图表信息,解决下列问题:
(1)m= , 解释m的实际意义:;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知10:00﹣11:00这个时段的借车数比还车数的一半还要多2,求此时段的借车数. 
查看答案和解析>>
科目: 来源: 题型:
【题目】图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα= ![]() .
. 
(1)求点M离地面AC的高度BM;
(2)设人站立点C与点A的水平距离AC=55cm,求铁环钩MF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com