
【题目】为进一步缓解城市交通压力,义乌市政府推出公共自行车,公共自行车在任何一个网店都能实现通租通还,某校学生小明统计了周六校门口停车网点各时段的借、还自行车数,以及停车点整点时刻的自行车总数(称为存量)情况,表格中x=1时的y的值表示8:00点时的存量,x=2时的y值表示9:00点时的存量…以此类推,他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
时段 | x | 还车数 | 借车数 | 存量y |
7:00﹣8:00 | 1 | 7 | 5 | 15 |
8:00﹣9:00 | 2 | 8 | 7 | n |
… | … | … | … | … |
根据所给图表信息,解决下列问题:
(1)m= , 解释m的实际意义:;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知10:00﹣11:00这个时段的借车数比还车数的一半还要多2,求此时段的借车数. 
【答案】
(1)13;7:00时自行车的存量
(2)解:由题意可得:n=15+8﹣7=16.
设二次函数关系式为y=ax2+bx+c,
∵二次函数图象过点(0,13)(1,15)(2,16),
∴  ,
,
∴a=﹣ ![]() ,b=
,b= ![]() ,c=13.
,c=13.
∴二次函数关系式为y=﹣ ![]() x2+
x2+ ![]() x+13
x+13
(3)解:将x=3,x=4代入得:y3=16,y4=15.
设还车数为x,则借车数为 ![]() +2.
+2.
根据题意得:y4=y3﹣( ![]() +2)即15=16﹣(
+2)即15=16﹣( ![]() +2)
+2)
解得x=2,
则 ![]() .
.
答:10:00﹣11:00这个时段的借车数为3辆
【解析】解:(1)m=15+5﹣7=13,m的实际意义:7:00时自行车的存量.
故答案为;13;7:00时自行车的存量.
(1)m表示7:00时自行车的存量,然后依据原有量=现存量+借车数﹣换车数求解即可;(2)将(0,13)(1,15)(2,16)的坐标代入函数的解析式可求得a、b、c的值,从而可求得二次函数的关系式;(3)将x=3,x=4代入得:y3=16,y4=15,设还车数为x,则借车数为 ![]() +2.接下来,依据题意列方程求解即可.
+2.接下来,依据题意列方程求解即可.


科目:初中数学 来源: 题型:
【题目】如图,A是∠MON边OM上一点,AE∥ON. 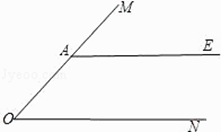
(1)在图中作∠MON的角平分线OB,交AE于点B;(要求:尺规作图,保留作图痕迹,不写作法和证明)
(2)在(1)中,过点A画OB的垂线,垂足为点D,交ON于点C,连接CB,将图形补充完整,并证明四边形OABC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF= ![]() CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
CD,以DE,DF为邻边作矩形DEGF.设AQ=3x. 
(1)用关于x的代数式表示BQ,DF.
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.
(3)在点P的整个运动过程中, ①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x﹣2的图象与反比例函数y2= ![]() 的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=
的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC= ![]() ,点B的坐标为(m,n),求反比例函数的解析式.
,点B的坐标为(m,n),求反比例函数的解析式. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P(t,0)(t>0)是x轴正半轴上的一点,是以原点为圆心,半径为1的 ![]() 圆,且A(﹣1,0),B(0,1),点M是
圆,且A(﹣1,0),B(0,1),点M是 ![]() 上的一个动点,连结PM,作直角△MPM1 , 并使得∠MPM1=90°,∠PMM1=60°,我们称点M1为点M的对应点.
上的一个动点,连结PM,作直角△MPM1 , 并使得∠MPM1=90°,∠PMM1=60°,我们称点M1为点M的对应点. 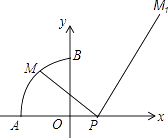
(1)设点A和点B的对应点为A1和B1 , 当t=1时,求A1的坐标;B1的坐标 .
(2)当P是x轴正半轴上的任意一点时,点M从点A运动至点B,求M1的运动路径长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对正方形纸片ABCD进行如下操作:
(I)过点D任作一条直线与BC边相交于点E1(如图①),记∠CDE1=a1;
(II)作∠ADE1的平分线交AB边于点E2(如图②),记∠ADE2=a2;
(III)作∠CDE2的平分线交BC边于点E3(如图③),记∠CDE3=a3;
按此作法从操作(2)起重复以上步骤,得到a1 , a2 , …,an , …,现有如下结论:
①当a1=10°时,a2=40°;
②2a4+a3=90°;
③当a5=30°时,△CDE9≌△ADE10;
④当a1=45°时,BE2= ![]() AE2 .
AE2 .
其中正确的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲从M地骑摩托车匀速前往N地,同时乙从N地沿同一条公路骑自行车匀速前往M地,甲到达N地后,原路原速返回,追上乙后返回到M地.设甲、乙与N地的距离分别为y1、y2千米,甲与乙之间的距离为s千米,设乙行走的时间为x小时.y1、y2与x之间的函数图象如图1. 
(1)分别求出y1、y2与x的函数表达式;
(2)求s与x的函数表达式,并在图2中画出函数图象;
(3)当两人之间的距离不超过5千米时,能够用无线对讲机保持联系.并且规定:持续联系时间不少于15分钟为有效联系时间.求当两人用无线对讲机保持有效联系时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,给出下列说法:①abc>0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③6a﹣b+c<0;④a﹣am2>bm﹣b,且m﹣1≠0,其中正确的说法有( ) 
A.①②③
B.②③④
C.①②④
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=﹣ ![]() x﹣1与反比例函数
x﹣1与反比例函数 ![]() (x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )
(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( ) 
A.﹣2
B.﹣4
C.﹣6
D.﹣8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com