
【题目】如图,点P(t,0)(t>0)是x轴正半轴上的一点,是以原点为圆心,半径为1的 ![]() 圆,且A(﹣1,0),B(0,1),点M是
圆,且A(﹣1,0),B(0,1),点M是 ![]() 上的一个动点,连结PM,作直角△MPM1 , 并使得∠MPM1=90°,∠PMM1=60°,我们称点M1为点M的对应点.
上的一个动点,连结PM,作直角△MPM1 , 并使得∠MPM1=90°,∠PMM1=60°,我们称点M1为点M的对应点. 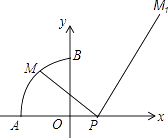
(1)设点A和点B的对应点为A1和B1 , 当t=1时,求A1的坐标;B1的坐标 .
(2)当P是x轴正半轴上的任意一点时,点M从点A运动至点B,求M1的运动路径长 .
【答案】
(1)(1,2 ![]() );(1+
);(1+ ![]() ,
, ![]() )
)
(2)![]()
【解析】解:(1)如图1, 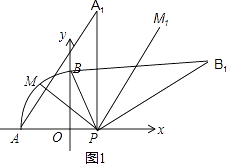
当t=1时,则AP=2,A1P⊥AP,
∵∠PAA1=60°,
∴PA1=2 ![]() ,
,
∴A1(1,2 ![]() ),
),
BP=OP= ![]() ,∠BPO=45°,
,∠BPO=45°,
∴∠B1PC=∠PBO=90°﹣∠BPO=45°,PC=B1C,
∵∠B1BP=60°,
∴PB1= ![]() ,
,
∴PC=B1C= ![]() ,
,
∴B1(1+ ![]() ,
, ![]() ),
),
所以答案是;(1,2 ![]() ),(1+
),(1+ ![]() ,
, ![]() );(2)当M在A点时,PM=1+t,PM1=(1+t)
);(2)当M在A点时,PM=1+t,PM1=(1+t) ![]() ,点M从点A运动至点B,设∠APB=n°,则PM1也旋转n°,
,点M从点A运动至点B,设∠APB=n°,则PM1也旋转n°,
∴M1的运动路径长= ![]() ,
,
∵ ![]() 的长=
的长= ![]() =
= ![]() =
= ![]() ,
,
∴M1的运动路径长= ![]() .
.
所以答案是: ![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知A1 , A2 , A3 , …,An是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1 , A2 , A3 , …,An+1作x轴的垂线交一次函数 ![]() 的图象于点B1 , B2 , B3 , …,Bn+1 , 连接A1B2 , B1A2 , A2B3 , B2A3 , …,AnBn+1 , BnAn+1依次产生交点P1 , P2 , P3 , …,Pn , 则Pn的坐标是 .
的图象于点B1 , B2 , B3 , …,Bn+1 , 连接A1B2 , B1A2 , A2B3 , B2A3 , …,AnBn+1 , BnAn+1依次产生交点P1 , P2 , P3 , …,Pn , 则Pn的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔试 | 面试 | 体能 | |
甲 | 83 | 79 | 90 |
乙 | 85 | 80 | 75 |
丙 | 80 | 90 | 73 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y= ![]() (x>0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,
(x>0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时, ![]() = .
= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG= ![]() cm,则EF的长为( )
cm,则EF的长为( ) 
A.2cm
B.![]() cm
cm
C.1cm
D.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步缓解城市交通压力,义乌市政府推出公共自行车,公共自行车在任何一个网店都能实现通租通还,某校学生小明统计了周六校门口停车网点各时段的借、还自行车数,以及停车点整点时刻的自行车总数(称为存量)情况,表格中x=1时的y的值表示8:00点时的存量,x=2时的y值表示9:00点时的存量…以此类推,他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
时段 | x | 还车数 | 借车数 | 存量y |
7:00﹣8:00 | 1 | 7 | 5 | 15 |
8:00﹣9:00 | 2 | 8 | 7 | n |
… | … | … | … | … |
根据所给图表信息,解决下列问题:
(1)m= , 解释m的实际意义:;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知10:00﹣11:00这个时段的借车数比还车数的一半还要多2,求此时段的借车数. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4). 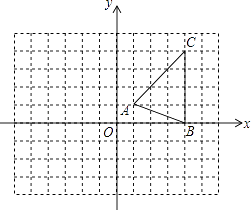
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2 .
(2)求点C1在旋转过程中所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品,C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图1和图2两幅尚不完整的统计图中. 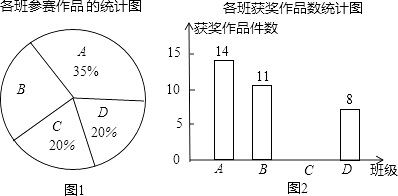
(1)B班参赛作品有多少件?
(2)请你将图2的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用如图所示的两个转盘进行“配紫色”游戏,每个转盘都被分成面积相等的三个扇形,游戏者同时转动两个转盘,配成紫色的概率是多少?请用树状图或列表说明理由(蓝色和红色能配成紫色). 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com