Question

【题目】如图，A是∠MON边OM上一点，AE∥ON．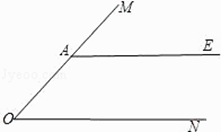
（1）在图中作∠MON的角平分线OB，交AE于点B；（要求：尺规作图，保留作图痕迹，不写作法和证明）
（2）在（1）中，过点A画OB的垂线，垂足为点D，交ON于点C，连接CB，将图形补充完整，并证明四边形OABC是菱形．

Answer 1

【答案】
（1）解：如图所示：

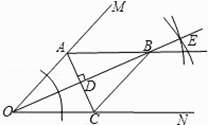
（2）证明：∵OB平分∠MON，

∴∠AOB=∠BOC．

∵AE∥ON，

∴∠ABO=∠BOC．

∴∠AOB=∠ABO，AO=AB．

∵AD⊥OB，

∴BD=OD．

在△ADB和△CDO中

∵

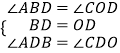
∴△ADB≌△CDO，AB=OC．

∵AB∥OC，

∴四边形OABC是平行四边形．

∵AO=AB，

∴四边形OABC是菱形．

【解析】（1）角平分线的作法：用圆规以顶点为圆心，任意长为半径画一个弧（要保证有两个交点，不要太小），再以刚才画出的交点为顶点，以大于第一次的半径为半径画弧（左右各画一个弧），再取两道弧的交点，并连接这个交点的一开始最上面的顶点，这就是角平分线．（2）本题可根据“一组邻边相等的平行四边形是菱形”，先证明OABC是个平行四边形，然后证明OA=AB即可．