问卷

你平时喝饮料吗？(　　)

A．不喝 　　　B．喝

请选择B选项的同学回答下面问题：

请您减少喝饮料的数量，将节省下来的钱捐给希望工程，您愿意平均每月少喝(　　)

A．0瓶 　　　B．1瓶

C．2瓶 　　　D．2瓶以上

根据上述信息，解答下列问题：

(1)求条形图中n的值．

(2)如果每瓶饮料平均3元钱，“少喝2瓶以上”按少喝3瓶计算：

①这2000名学生一个月少喝饮料能节省多少钱捐给希望工程？

②按上述统计结果估计，该市七年级6万名学生一个月少喝饮料大约能节省多少钱捐给希望工程？

【题目】阅读与思考 婆罗摩笈多（Brahmagupta），是一位印度数学家和天文学家，书写了两部关于数学和天文学的书籍，他的一些数学成就在世界数学史上有较高的地位，他的负数概念及加减法运算仅晚于中国《九章算术》，而他的负数乘除法法则在全世界都是领先的，他还提出了著名的婆罗摩笈多定理，该定理的内容及部分证明过程如下：
已知：如图1，四边形ABCD内接于⊙O，对角线AC⊥BD于点P，PM⊥AB于点M，延长MP交CD于点N，求证：CN=DN．
证明：在△ABP和△BMP中，∵AC⊥BD，PM⊥AB，
∴∠BAP+∠ABP=90°，∠BPM+∠MBP=90°．
∴∠BAP=∠BPM．
∵∠DPN=∠BPM，∠BAP=∠BDC．
∴…

（1）请你阅读婆罗摩笈多定理的证明过程，完成剩余的证明部分．
（2）已知：如图2，△ABC内接于⊙O，∠B=30°，∠ACB=45°，AB=2，点D在⊙O上，∠BCD=60°，连接AD，与BC交于点P，作PM⊥AB于点M，延长MP交CD于点N，则PN的长为 ．

【题目】如图，以原点O为圆心，3为半径的圆与x轴分别交于A，B两点（点B在点A的右边），P是半径OB上一点，过P且垂直于AB的直线与⊙O分别交于C，D两点（点C在点D的上方），直线AC，DB交于点E．若AC：CE=1：2．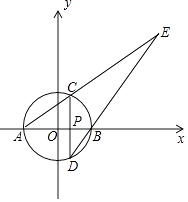
（1）求点P的坐标；
（2）求过点A和点E，且顶点在直线CD上的抛物线的函数表达式．

已知商家售出的2台A型、3台B型污水处理器的总价为44万元，售出的1台A型、4台B型污水处理器的总价为42万元．
（1）求每台A型、B型污水处理器的价格；
（2）为确保将每月产生的污水全部处理完，该企业决定购买上述的污水处理器，那么他们至少要支付多少钱？

【题目】操作：“如图1，P是平面直角坐标系中一点（x轴上的点除外），过点P作PC⊥x轴于点C，点C绕点P逆时针旋转60°得到点Q．”我们将此由点P得到点Q的操作称为点的T变换．

（1）点P（a，b）经过T变换后得到的点Q的坐标为 ；若点M经过T变换后得到点N（6，﹣ ），则点M的坐标为 ．
（2）A是函数y= x图象上异于原点O的任意一点，经过T变换后得到点B．
①求经过点O，点B的直线的函数表达式；
②如图2，直线AB交y轴于点D，求△OAB的面积与△OAD的面积之比．

A. y=kx﹣2（k≠0） B. y=kx+k+2（k≠0）

C. y=kx﹣k+2（k≠0） D. y=kx+k﹣2（k≠0）

【题目】如图，已知等边△ABC，请用直尺（不带刻度）和圆规，按下列要求作图（不要求写作法，但要保留作图痕迹）：
（1）作△ABC的外心O；
（2）设D是AB边上一点，在图中作出一个正六边形DEFGHI，使点F，点H分别在边BC和AC上．

A. B. ﹣ C. ﹣4或4 D. ﹣或

（1）已知x﹣2的平方根是±2，2x+y+7的立方根是3，求x2+y2的平方根．

（2）已知实数a、b满足（a﹣2）2+=0，求b﹣a的算术平方根

（3）已知y=，求的值

【题目】在正方形网格中，我们把，每个小正方形的顶点叫做格点，连接任意两个格点的线段叫网格线段，以网格线段为边组成的图形叫做格点图形，在下列如图所示的正方形网格中，每个小正方形的边长为1．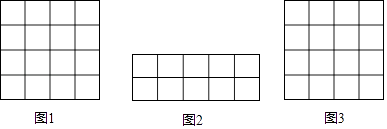
（1）请你在图1中画一个格点图形，且该图形是边长为 的菱形；
（2）请你在图2中用网格线段将其切割成若干个三角形和正方形，拼接成一个与其面积相等的正方形，并在图3中画出格点正方形．