
科目: 来源: 题型:
【题目】已知:如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB与EF的位置关系,并说明理由.
解: ,理由如下:
∵AB∥CD,
∴∠B=∠BCD,( )
∵∠B=70°,
∴∠BCD=70°,( )
∵∠BCE=20°,
∴∠ECD=50°,
∵∠CEF=130°,
∴ + =180°,
∴EF∥ ,( )
∴AB∥EF.( )

查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,分别交BC,AD于E,F两点,交BA的延长于G,判断弧EF和弧FG是否相等,并说明理由。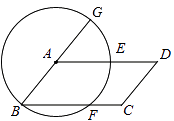
查看答案和解析>>
科目: 来源: 题型:
【题目】计算下列各题:
(1)(﹣1)2018+3﹣2﹣(π﹣3.14)0
(2)(x+3)2﹣x2
(3)(x+2)(3x﹣y)﹣3x(x+y)
(4)(2x+y+1)(2x+y﹣1)
查看答案和解析>>
科目: 来源: 题型:
【题目】如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”。如图,在三角形ABC中,∠C=90°,较短的一条直角边BC=1,且三角形ABC是“有趣三角形”,求三角形ABC的“有趣中线”的长。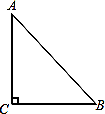
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的任意一动点,点
边上的任意一动点,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,直线
对称,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)求![]() 边上的高;
边上的高;
(2)当![]() 为何值时,△
为何值时,△![]() 与△
与△![]() 重叠部分的面积最大,并求出最大值;
重叠部分的面积最大,并求出最大值;
(3)连接![]() ,当
,当![]() 为直角三角形时,求
为直角三角形时,求![]() 的度数.
的度数.



查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读与思考:
整式乘法与因式分解是方向相反的变形,由![]()
![]() ,
,
可得 ![]() .
.
利用这个式子可以将某些二次项系数是1的二次三项式分解因式.
例如:将式子![]() 分解因式.
分解因式.
这个式子的常数项![]() ,一次项系
,一次项系![]() ,
,
所以![]() .
.

解:![]()
![]() .
.
上述分解因式![]() 的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如右图).
的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如右图).
请仿照上面的方法,解答下列问题:
(1)分解因式:![]() =___________________;
=___________________;
(2)若![]() 可分解为两个一次因式的积,则整数P的所有可能值是________.
可分解为两个一次因式的积,则整数P的所有可能值是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知平面内一点P,若点P到两条相交直线l1和l2的距离都相等,且距离均为h(h>0),则称点P叫做直线l1和l2的“h距离点”. 例如图1所示,直线l1和l2互相垂直,交于O点,平面内一点P到两直线的距离都是2,则称点P叫做直线l1和l2的“2距离点”.
(1)若直线l1和l2互相垂直,且交于O点,平面内一点P是直线l1和l2的“7距离点”,直接写出OP的长度为 ;
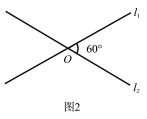
(2)如图2所示,直线l1和l2相交于点O,夹角为60°,已知平面内一点P是直线l1和l2的“3距离点”,求出OP的长度;
(3)已知三条直线两两相交后形成一个等边三角形,如图3所示,在等边△ABC中,点P是三角形内部一点,且点P分别是等边△ABC三边所在直线的“![]() 距离点”,请你直接写出△ABC的面积是 .
距离点”,请你直接写出△ABC的面积是 .


查看答案和解析>>
科目: 来源: 题型:
【题目】小明四等分弧AB,他的作法如下:
①连接AB(如图);作AB的垂直平分线CD交弧AB于点M,交AB于点T;
②分别作AT,TB的垂直平分线EF,GH,交弧AB于N,P两点,则N,M,P三点把弧AB四等分。你认为小明的作法是否正确: , 理由是。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com