
科目: 来源: 题型:
【题目】如图,已知∠MAN=120°,AC平分∠MAN.B、D分别在射线AN、AM上.
(1)在图1中,当∠ABC=∠ADC=90°时,求证:AD+AB=AC
(2)若把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,如图2所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

(图1) (图2)
查看答案和解析>>
科目: 来源: 题型:
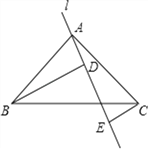
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l于D,CE⊥AE,若BD>CE,试问:
(1)AD与CE的大小关系如何?请说明理由;
(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】白色污染(White Pollution)是人们对难降解的塑料垃圾(多指塑料袋)污染环境现象的一种形象称谓.为了让全校同学感受丢弃塑料袋对环境的影响,小彬随机抽取某小区![]() 户居民,记录了这些家庭
户居民,记录了这些家庭![]() 年某个月丢弃塑料袋的数量(单位:个):
年某个月丢弃塑料袋的数量(单位:个):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
请根据上述数据,解答以下问题:
(1)小彬按“组距为![]() ”列出了如下的频数分布表(每组数据含最小值),请将表中空缺的部分补充完整,并补全频数直方图;
”列出了如下的频数分布表(每组数据含最小值),请将表中空缺的部分补充完整,并补全频数直方图;
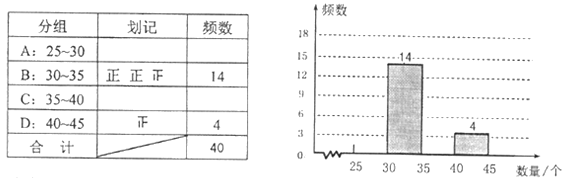
(2)根据(1)中的直方图可以看出,这![]() 户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
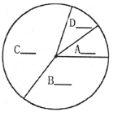
(3)根据频数分布表,小彬又画出了右图所示的扇形统计图.请将统计图中各组占总数的百分比填在图中,并求出![]() 组对应的扇形圆心角的度数;
组对应的扇形圆心角的度数;
(4)若小区共有![]() 户居民家庭,请你估计每月丢弃的塑料袋数量不小于
户居民家庭,请你估计每月丢弃的塑料袋数量不小于![]() 个家庭个数.
个家庭个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目: 来源: 题型:
【题目】李明上星期买进某公司股票7000股,每股27元,下表为本周每日该股票的涨跌情况![]() 单位:元
单位:元![]()
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌 |
|
|
|
|
|
|
![]() 这六天中,哪几天的股票是上涨的?哪几天的股票是下跌的?
这六天中,哪几天的股票是上涨的?哪几天的股票是下跌的?
![]() 哪天股票上涨的最多?你能算出这天收盘时每股是多少元吗?
哪天股票上涨的最多?你能算出这天收盘时每股是多少元吗?
![]() 本周六收盘时每股是多少元?
本周六收盘时每股是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】李老师给爱好学习的小兵和小鹏提出这样一个问题:如图1,在△ABC中,AB=AC点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
小兵的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小鹏的证明思路是:如图2,过点P作PG⊥CF,垂足为G,先证△GPC≌△ECP,可得:PE=CG,而PD=GF,则PD+PE=CF.
请运用上述中所证明的结论和证明思路完成下列两题:
(1)如图3,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=16,CF=6,求PG+PH的值;
(2)如图4,P是边长为6的等边三角形ABC内任一点,且PD⊥AB,PF⊥AC,PE⊥BC,求PD+PE+PF的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点![]() 在线段
在线段![]() 上.点
上.点![]() 从点
从点![]() 出发向点
出发向点![]() 运动,速度为2cm/s;同时,点
运动,速度为2cm/s;同时,点![]() 也从点
也从点![]() 出发用1s到达
出发用1s到达![]() 处,并在
处,并在![]() 处停留2s,然后按原速度向点
处停留2s,然后按原速度向点![]() 运动,速度为4cm/s.最终,点
运动,速度为4cm/s.最终,点![]() 比点
比点![]() 早1s到达
早1s到达![]() 处.设点
处.设点![]() 运动的时间为
运动的时间为![]() s.
s.
(1)线段![]() 的长为 cm;当
的长为 cm;当![]() =3s时,
=3s时,![]() 两点之间的距离为 cm;
两点之间的距离为 cm;
(2)求线段![]() 的长;
的长;
(3)从![]() 两点同时出发至点
两点同时出发至点![]() 到达点
到达点![]() 处的这段时间内,
处的这段时间内,![]() 为何值时,
为何值时,![]() 两点相距1 cm?
两点相距1 cm?
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某校八年级举行英语演讲比赛,购买A,B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元.根据比赛设奖情况,需购买笔记本共30本,并且所购买A笔记本的数量要不多于B笔记本数量的![]() ,但又不少于B笔记本数量
,但又不少于B笔记本数量![]() ,设买A笔记本n本,买两种笔记本的总费为w元.
,设买A笔记本n本,买两种笔记本的总费为w元.
(1)写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;
(2)购买这两种笔记本各多少时,费用最少?最少的费用是多少元?
(3)商店为了促销,决定仅对A种类型的笔记本每本让利a元销售,B种类型笔记本售价不变.问购买这两种笔记本各多少本时花费最少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某市实施居民用水阶梯价格制度,按年度用水量计算,将居民家庭全年用水量划分为三个阶梯,水价按阶梯递增:
第一阶梯:年用水量不超过200吨,每吨水价为3元;
第二阶梯:年用水量超过200吨但不超过300吨的部分,每吨水价为3. 5元;
第三阶梯:年用水量超过300吨的部分,每吨水价为6元.
(1)小明家2018年用水180吨,这一年应缴纳水费 元;
(2)小亮家2018年缴纳水费810元,则小亮家这一年用水多少吨?
(3)小红家2017年和2018年共用水600吨,共缴纳水费1950元,并且2018年的用水量超过2017年的用水量,则小红家2017年和2018年各用水多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com