
科目: 来源: 题型:
【题目】为方便市民通行,某广场计划对坡角为30°,坡长为60米的斜坡AB进行改造,在斜坡中点D处挖去部分坡体(阴影表示),修建一个平行于水平线CA的平台DE和一条新的斜坡BE.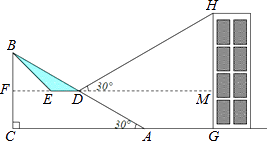
查看答案和解析>>
科目: 来源: 题型:
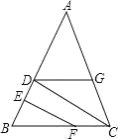
【题目】如图,AB∥CD.∠1=∠2,∠3=∠4,试说明 AD∥BE,请你将下面解答过程填写完整.

解:∵AB∥CD,
∴∠4= ( )
∵∠3=∠4
∴∠3= (等量代换)
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAE 即∠BAE= .
∴∠3= ( )
∴AD∥BE( ).
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.
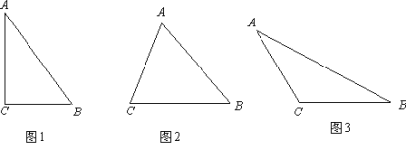
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米.(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了5米,那么梯子的底端在水平方向滑动了多少米?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
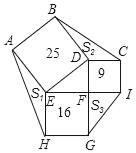
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,圆柱底面半径为![]() cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A. 12cm B. ![]() cm C. 15cm D.
cm C. 15cm D. ![]() cm
cm
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,长方形 BCDE 的各边分别平行于 x 轴或 y 轴,物体甲和物体乙分别由点 A(2,0)同时出发,沿长方形 BCDE 的边作环绕运动,物体甲按逆时针方向以 1 个单位/秒匀速运动,物体乙按顺时针方向以 2 个单位/秒匀速运动,则两个物体运动后的第 2020 次相遇地点的坐标是_____.
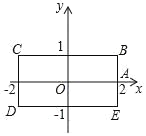
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:
①分别以A,C为圆心,a为半径(a>![]() AC)作弧,两弧分别交于M,N两点;
AC)作弧,两弧分别交于M,N两点;
②过M,N两点作直线MN交AB于点D,交AC于点E;
③将△ADE绕点E顺时针旋转180°,设点D的像为点F.

(1)请在图中直线标出点F并连接CF;
(2)求证:四边形BCFD是平行四边形;
(3)当∠B为多少度时,四边形BCFD是菱形.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙、丙、丁一起研究一道数学题,如图,已知 EF⊥AB,CD⊥AB,甲说:“如果还知道∠CDG=∠BFE,则能得到∠AGD=∠ACB.”乙说:“如果还知道∠AGD=∠ACB,则能得到∠CDG=∠BFE.”丙说:“∠AGD 一定大于∠BFE.”丁说:“如果连接 GF,则 GF∥AB.”他们四人中,正确的是( )
A.0 个B.1 个C.2 个D.3 个
查看答案和解析>>
科目: 来源: 题型:
【题目】疫情期间,为满足口罩需求,某商店决定购进A,B两种口罩。若购进A口罩10盒,B口罩5盒,需要1000元。若购进A口罩4盒,B口罩3盒,需要550元.
(1)求A,B两种口罩每盒需要多少元?
(2)若该商店决定拿出10000元全部用来购进这两种口罩,考虑到市场需求,要求购进A口罩的数量不少于B口罩数量的6倍,且不超过B口罩数量的8倍,那么该商店共有几种进货方案?
(3)若销售每盒A口罩可以获利润20元,每盒B口罩可以获利润30元,在(2)的各种进货方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com