
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,BD=8cm.点M从点A出发,沿AC的方向匀速运动,同时直线PQ由点B出发,沿BA的方向匀速运动,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t≤5).线段CM的长度记作y甲 , 线段BP的长度记作y乙 , y甲和y乙关于时间t的函数变化情况如图所示.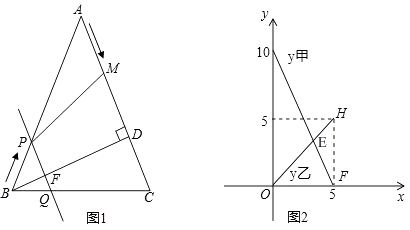
(1)由图2可知,点M的运动速度是每秒cm,当t为何值时,四边形PQCM是平行四边形?在图2中反映这一情况的点是;
(2)设四边形PQCM的面积为ycm2 , 求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PQCM= ![]() S△ABC?若存在,求出t的值;若不存在,说明理由;
S△ABC?若存在,求出t的值;若不存在,说明理由;
(4)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OM⊥AB.
(1)∠AOC的邻补角为 (写出一个即可);
(2)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(3)若∠1=![]() ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
(1)正方形ABCD的面积为 ,边长为 ,对角线BD= ;
(2)求证:![]() ;
;
(3)如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 ,若点E所表示的数为整数,则点E所表示的数为 .


查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),直接写出线段AD与NE的数量关系为 . 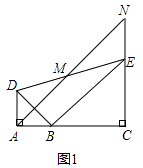
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),判断△ACN是什么特殊三角形并说明理由.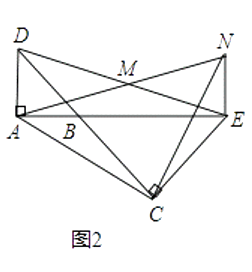
(3)将图1中△BCE绕点B旋转到图3位置,此时A,B,M三点在同一直线上.若AC=3 ![]() ,AD=1,则四边形ACEN的面积为 .
,AD=1,则四边形ACEN的面积为 . 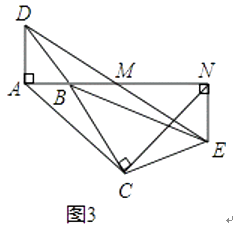
查看答案和解析>>
科目: 来源: 题型:
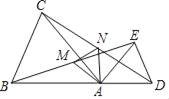
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在同一条直线上,M,N分别为BE,CD的中点.
(1)求证:△ABE≌ACD;
(2)判断△AMN的形状,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S=![]() ACBD.
ACBD.
正确的是 (填写所有正确结论的序号)

查看答案和解析>>
科目: 来源: 题型:
【题目】a是不为1的有理数,我们把![]() 称为a的差倒数.如:2的差倒数是
称为a的差倒数.如:2的差倒数是![]() ,现已知a1=
,现已知a1=![]() ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…
(1)求a2,a3,a4的值;
(2)根据(1)的计算结果,请猜想并写出a2016a2017a2018的值;
(3)计算:a33+a66+a99+…+a9999的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,点A为半圆O直径MN所在直线上一点,射线AB垂直于MN,垂足为A,半圆绕M点顺时针转动,转过的角度记作a;设半圆O的半径为R,AM的长度为m,回答下列问题: 
探究:
(1)若R=2,m=1,如图1,当旋转30°时,圆心O′到射线AB的距离是;如图2,当a=°时,半圆O与射线AB相切;
(2)如图3,在(1)的条件下,为了使得半圆O转动30°即能与射线AB相切,在保持线段AM长度不变的条件下,调整半径R的大小,请你求出满足要求的R,并说明理由. 
(3)发现:如图4,在0°<α<90°时,为了对任意旋转角都保证半圆O与射线AB能够相切,小明探究了cosα与R、m两个量的关系,请你帮助他直接写出这个关系;cosα=(用含有R、m的代数式表示) 
(4)拓展:如图5,若R=m,当半圆弧线与射线AB有两个交点时,α的取值范围是 , 并求出在这个变化过程中阴影部分(弓形)面积的最大值(用m表示) 
查看答案和解析>>
科目: 来源: 题型:
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发匀速前行,且途中休息一段时间后继续以原速前行.家到公园的距离为2000m,如图是小明和爸爸所走的路程S(m)与步行时间t(min)的函数图象.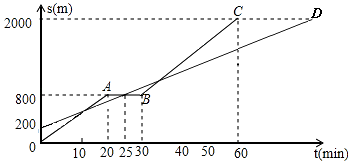
(1)直接写出BC段图象所对应的函数关系式(不用写出t的取值范围).
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早18分钟到达公园,则小明在步行过程中停留的时间需减少分钟.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com