
����Ŀ����ͼ��ʾ����AΪ��ԲOֱ��MN����ֱ����һ�㣬����AB��ֱ��MN������ΪA����Բ��M��˳ʱ��ת����ת���ĽǶȼ���a�����ԲO�İ뾶ΪR��AM�ij���Ϊm���ش��������⣺ 
̽����
��1����R=2��m=1����ͼ1������ת30��ʱ��Բ��O�䵽����AB�ľ���������ͼ2����a=��ʱ����ԲO������AB���У�
��2����ͼ3���ڣ�1���������£�Ϊ��ʹ�ð�ԲOת��30�㼴��������AB���У��ڱ����߶�AM���Ȳ���������£������뾶R�Ĵ�С�������������Ҫ���R����˵�����ɣ� 
��3�����֣���ͼ4����0�㣼����90��ʱ��Ϊ�˶�������ת�Ƕ���֤��ԲO������AB�ܹ����У�С��̽����cos����R��m�������Ĺ�ϵ�����������ֱ��д�������ϵ��cos��=���ú���R��m�Ĵ���ʽ��ʾ�� 
��4����չ����ͼ5����R=m������Բ����������AB����������ʱ������ȡֵ��Χ�� �� �����������仯��������Ӱ���֣����Σ���������ֵ����m��ʾ�� 
���𰸡�
��1��![]() +1��60��
+1��60��
��2���⣺���е�ΪP������O��P����MQ��O��P�����ı���APQM�Ǿ��Σ�

��O��P=R��
��R= ![]() R+1��
R+1��
��R=4+2 ![]() ��
��
��3��![]()
��4���⣺��ͼ5��, ����Բ������AB����ʱ,֮��ʼ������������,��ʱ��=90�㣻��N������AB��ʱ,Ϊ��Բ��AB��������������ʱ��,��ʱ��MN��=2AM,���ԡ�AMN��=60��,����,��=120�����,����Բ����������AB����������ʱ,����ȡֵ��Χ�ǣ�90�㣼����120��ʴ�Ϊ90�㣼����120�㣻��N������AB��ʱ,��Ӱ����������,����S�T
����Բ������AB����ʱ,֮��ʼ������������,��ʱ��=90�㣻��N������AB��ʱ,Ϊ��Բ��AB��������������ʱ��,��ʱ��MN��=2AM,���ԡ�AMN��=60��,����,��=120�����,����Բ����������AB����������ʱ,����ȡֵ��Χ�ǣ�90�㣼����120��ʴ�Ϊ90�㣼����120�㣻��N������AB��ʱ,��Ӱ����������,����S�T ![]() ��
�� ![]() ?
? ![]() m?
m? ![]() m=
m= ![]() ��
�� ![]() m2��
m2��
���������⣺��1����ͼ1�У���O��E��AB��E��MF��O��E��F�����ı���AMFE�Ǿ��Σ�EF=AM=1����취���O��E�ij����ɣ�

��Rt��MFO���У��ߡ�MO ![]() F=30�㣬MO��=2��
F=30�㣬MO��=2��
��O��F=O��Mcos30��= ![]() ��O��E=
��O��E= ![]() +1��
+1��
���O�䵽AB�ľ���Ϊ ![]() +1��
+1��
��ͼ2�У����е�ΪF������O��F����O��E��OA��E�����ı���O��EAF�Ǿ��Σ�

��AE=O��F=2��
��AM=1��
��EM=1��
��Rt��O��EM��sin��= ![]() =
= ![]() ��
��
���=60��
�ʴ�Ϊ ![]() +1��60�㣮��3�����е�ΪP������O��P����MQ��O��P�����ı���APQM�Ǿ��Σ�
+1��60�㣮��3�����е�ΪP������O��P����MQ��O��P�����ı���APQM�Ǿ��Σ�

��Rt��O��QM��O��Q=Rcos����QP=m��
��O��P=R��
��Rcos��+m=R��
��cos��= ![]() ��
��
�ʴ�Ϊ ![]() ��
��
��1����ͼ1�У���O��E��AB��E��MF��O��E��F�����ı���AMFE�Ǿ��Σ�EF=AM=1����ͼ2�У����е�ΪF������O��F����O��E��OA��E�����ı���O��EAF�Ǿ��Σ���Rt��O��EM�У���sin��= ![]() =
= ![]() ���Ƴ���=60�㣮��2�����е�ΪP������O��P����MQ��O��P�����ı���APQM�Ǿ��Σ��г����̼��ɽ�����⣮��3�����е�ΪP������O��P����MQ��O��P�����ı���APQM�Ǿ��Σ��г����̼��ɽ�����⡢��4������Բ������AB����ʱ��֮��ʼ�����������㣬��ʱ��=90�㣻��N������AB��ʱ��Ϊ��Բ��AB��������������ʱ�̣���ʱ��MN��=2AM�����ԡ�AMN��=60�㣬���ԣ���=120����ˣ�����Բ����������AB����������ʱ������ȡֵ��Χ�ǣ�90�㣼����120�㣮��N������AB��ʱ����Ӱ���������������ʱ��������ɣ�
���Ƴ���=60�㣮��2�����е�ΪP������O��P����MQ��O��P�����ı���APQM�Ǿ��Σ��г����̼��ɽ�����⣮��3�����е�ΪP������O��P����MQ��O��P�����ı���APQM�Ǿ��Σ��г����̼��ɽ�����⡢��4������Բ������AB����ʱ��֮��ʼ�����������㣬��ʱ��=90�㣻��N������AB��ʱ��Ϊ��Բ��AB��������������ʱ�̣���ʱ��MN��=2AM�����ԡ�AMN��=60�㣬���ԣ���=120����ˣ�����Բ����������AB����������ʱ������ȡֵ��Χ�ǣ�90�㣼����120�㣮��N������AB��ʱ����Ӱ���������������ʱ��������ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC����AB��AC����BAC��90�㣬��1����2��CE��BD��BD���ӳ����ڵ�E.��֤��BD��2CE.
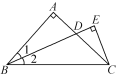
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����߳�Ϊ3�������εĶԽ��߳�Ϊa�����й���a������˵���� ��a����������
��a�����������ϵ�һ��������ʾ��
��3��a��4��
��a��18������ƽ������
���У�������ȷ˵��������ǣ� ��
A.�٢�
B.�ڢ�
C.�٢ڢ�
D.�٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=2x+4��ͼ�����ͼ�����������⣺
(1)д������2x+4=0�Ľ⣻
(2)����4��yʱ������Ӧx��ȡֵ��Χ��
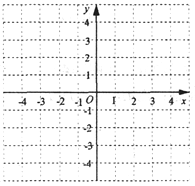
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��רҵ���ƻ�Ͷ����ֲ���ܼ���ľ�������г�������Ԥ�⣬��ֲ��ľ������y1��Ͷ����x����������ϵ����ֲ���ܵ�����y2��Ͷ����x��ƽ������������ϵ�����õ��˱����е����ݣ�
Ͷ����x����Ԫ�� | 2 |
��ֲ��ľ����y1����Ԫ�� | 4 |
��ֲ��������y2����Ԫ�� | 2 |
��1���ֱ��������y1��y2����Ͷ����x�ĺ�����ϵʽ��
��2�������λרҵ����8��Ԫ�ʽ�Ͷ����ֲ���ܺ���ľ������Ͷ����ֲ���ܽ��m��Ԫ����ֲ���ܺ���ľ����������W��Ԫ��ֱ��д��W����m�ĺ�����ϵʽ�����������ٻ�ö����������ܻ�ȡ����������Ƕ��٣�
��3������רҵ�������������22���ڣ�2���������£�ֱ��д��Ͷ����ֲ���ܵĽ��m�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��CD��CE��AB�ڵ�F������E=20������C=45�������A�Ķ���Ϊ��������

A. 5�� B. 15�� C. 25�� D. 35��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����OABC�У�OΪƽ��ֱ������ϵ��ԭ�㣬��A����C�ֱ���x�ᣬy���ϣ���B����Ϊ��4��6������P�ӵ�O��������ÿ��2����λ���ȵ��ٶ���O��C��B�����˶�������Bֹͣ�����P�˶���ʱ��Ϊt���룩��
��1����A����������������
��2����t=1��ʱ����P����������������
��3������P��OC���˶�����ֱ��д����P�����꣨�ú���t��ʽ�ӱ�ʾ����
��4�����ƶ������У�����P��y��ľ���Ϊ1����λ����ʱ����t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ٰ���ӭʡ����ѧ���黭չ������Ҫ�ڳ�����չ���л���![]() ����״����С��ȫһ����С������(����Ӱ����)���ǰڷ�չ����Ʒ��
����״����С��ȫһ����С������(����Ӱ����)���ǰڷ�չ����Ʒ��
��1����ͼ1�������εij��Ϳ��քeΪ![]() ��
��![]() �ף���С�����εij��Ϳ���
�ף���С�����εij��Ϳ���

��2����ͼ2�������εij��Ϳ��ֱ�Ϊ![]() ��
��![]() �����һ��С��������һ�������ܳ��ı�ֵ��
�����һ��С��������һ�������ܳ��ı�ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��ڵȱ�������ABC�У�D��AB���ϵĶ��㣬��CDΪһ�ߣ��������ȱ�������EDC������AE.
(l)��֤����DBC����EAC
(2)��˵��AE��BC�����ɣ�
(3)��ͼ�ڣ���ͼ���ж���D�˶�����BA���ӳ�����ʱ��������Ϊ�ȱ������Σ������Ƿ�����AE��BC?��������֤����


�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com