∵EF∥AD，（　 　）

∴∠2＝　 　．（两直线平行，同位角相等）

又∵∠1＝∠2，（　 　）

∴∠1＝∠3．（　 　）

∴AB∥DG．（　 　）

∴∠BAC+　 　＝180°（　 　）

又∵∠BAC＝70°，（　 　）

∴∠AGD＝　 　．

A．4cm2 B．6cm2 C．8cm2 D．9cm2

（1）甲、乙同时出发，背向而行，问几小时后他们相距351千米？

（2）甲、乙相向而行，甲出发三小时后乙才出发，问乙出发几小时后两人相遇？

（3）甲、乙相向而行，要使他们相遇于AB的中点，乙要比甲先出发几小时？

（4）甲、乙同时出发，相向而行，甲到达B处，乙到达A处都分别立即返回，几小时后相遇？相遇地点距离A有多远？

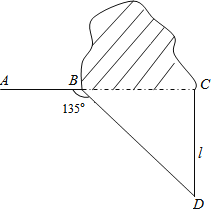
【题目】如图，修公路遇到一座山，于是要修一条隧道．为了加快施工进度，想在小山的另一侧同时施工．为了使山的另一侧的开挖点C在AB的延长线上，设想过C点作直线AB的垂线L，过点B作一直线（在山的旁边经过），与L相交于D点，经测量∠ABD=135°，BD=800米，求直线L上距离D点多远的C处开挖？（≈1.414，精确到1米）

（1）请计算最喜欢B项目的人数所占的百分比．

（2）请计算D项所在扇形图中的圆心角的度数．

（3）请把统计图补充完整．

（1）求甲、乙两车间各有多少人？

（2）若从甲、乙两车间分别抽调工人，组成丙车间研制新产品，并使甲、乙、丙三个车间的人数比为13∶4∶7，那么甲、乙两车间要分别抽调多少工人？

【题目】如图，一块余料ABCD，AD∥BC，现进行如下操作：以点B为圆心，适当长为半径画弧，分别交BA，BC于点G，H；再分别以点G，H为圆心，大于GH的长为半径画弧，两弧在∠ABC内部相交于点O，画射线BO，交AD于点E．

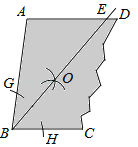
（1）求证：AB=AE；

（2）若∠A=100°，求∠EBC的度数．

【题目】5月19日为中国旅游日，衢州推出“读万卷书，行万里路，游衢州景”的主题系列旅游惠民活动，市民王先生准备在优惠日当天上午从孔氏南宗家庙、烂柯山、龙游石窟中随机选择一个地点；下午从江郎山、三衢石林、开化根博园中随机选择一个地点游玩，则王先生恰好上午选中孔氏南宗家庙，下午选中江郎山这两个地的概率是（ ）
A.
B.
C.
D.

① 求证：△ABE≌△CBD；

② 若∠CAE＝30°，求∠BDC的度数．

（1）如图1，是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，试用不同的方法计算这个图形的面积，你能发现什么结论，请写出来．

（2）如图2，是将两个边长分别为a和b的正方形拼在一起，B、C、G三点在同一直线上，连接BD和BF，若两正方形的边长满足a+b=10，ab=20，你能求出阴影部分的面积吗？