
科目: 来源: 题型:
【题目】如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE. 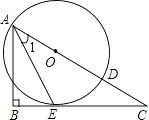
(1)求证:AE平分∠CAB;
(2)探求图中∠1与∠C的数量关系,并求当AE=EC时tanC的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(c2012防城港)某奶品生产企业,2010年对铁锌牛奶、酸牛奶、纯牛奶三个品种的生产情况进行了统计,绘制了图1、2的统计图,请根据图中信息解答下列问题: 
(1)酸牛奶生产了多少万吨?把图1补充完整;酸牛奶在图2所对应的圆心角是多少度?
(2)由于市场不断需求,据统计,2011年的生产量比2010年增长20%,按照这样的增长速度,请你估算2012年酸牛奶的生产量是多少万吨?
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图![]() 示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
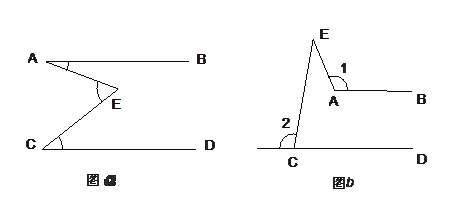
(2)现在如图b示,仍有AB∥CD,但点E在AB与CD的上方,①请尝试探索∠1,∠2,∠E三者的数量关系. ②请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等腰△ABC的顶角∠A=36°(如图). 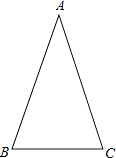
(1)作底角∠ABC的平分线BD,交AC于点D(用尺规作图,不写作法,但保留作图痕迹,然后用墨水笔加墨);
(2)通过计算说明△ABD和△BDC都是等腰三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=﹣(x﹣2)2+ ![]() 的图象与x轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有个(提示:必要时可利用下面的备用图画出图象来分析).
的图象与x轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有个(提示:必要时可利用下面的备用图画出图象来分析). 
查看答案和解析>>
科目: 来源: 题型:
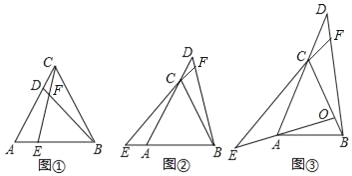
【题目】(1)在等边三角形ABC中,
①如图①,D,E分别是边AC,AB上的点且AE=CD,BD与EC交于点F,则∠BFE的度数是 度;
②如图②,D,E分别是边AC,BA延长线上的点且AE=CD,BD与EC的延长线交于点F,此时∠BFE的度数是 度;
(2)如图③,在△ABC中,AC=BC,∠ACB是锐角,点O是AC边的垂直平分线与BC的交点,点D,E分别在AC,OA的延长线上,AE=CD,BD与EC的延长线交于点F,若∠ACB=α,求∠BFE的大小.(用含α的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字﹣1、1、2.随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮与3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?
(2)某蔬菜公司的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元,当地一家公司收购这种蔬菜140吨,该公司的加工生产能力是:如果对蔬菜进行粗加工,每天可加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天将这批蔬菜全部销售或加工完毕,为此公司研制了三种可行方案:
方案一:将蔬菜全部进行粗加工.
方案二:尽可能多地对蔬菜进行精加工,没来得及进行加工的蔬菜,在市场上直接销售.
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为哪种方案获利最多?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图,点C、D在线段AB上,D是线段AB的中点,AC=![]() AD ,CD=4 ,求线段AB的长.
AD ,CD=4 ,求线段AB的长.
![]()
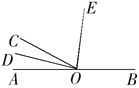
(2)如图,点O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB的平分线,若∠AOD=14°,求∠DOE、∠BOE的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在△ABC中,D是BA延长线上一点,AE是∠DAC的平分线,P是AE上的一点(点P不与点A重合),连接PB,PC.通过观察,测量,猜想PB+PC与AB+AC之间的大小关系,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com