
科目: 来源: 题型:
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
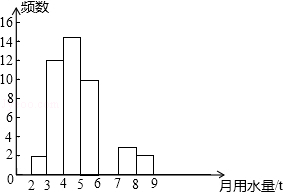
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合题。
(1)如图1,已知AD=BC,AC=BD.求证:△ADB≌△BCA. 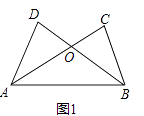
(2)如图2,已知AB是⊙O的一条直径,延长AB至点C,使AC=3BC,CD与⊙O相切于点D,若CD= ![]() ,求⊙O的半径.
,求⊙O的半径. 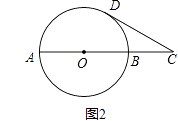
查看答案和解析>>
科目: 来源: 题型:
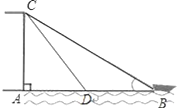
【题目】已知:如图,有人在岸上点C的地方,用绳子拉船靠岸,开始时,绳长CB=10米,CA⊥AB,且CA=6米,拉动绳子将船从点B沿BA方向行驶到点D后,绳长CD=6![]() 米.
米.
(1)试判定△ACD的形状,并说明理由;
(2)求船体移动距离BD的长度.

查看答案和解析>>
科目: 来源: 题型:
【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如下图),再分别依次从左到右取2个,3个,4个,5个正方形拼成如下长方形并记为①,②,③,④,相应长方形的周长如下表所示:
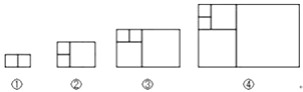

若按此规律继续作长方形,则序号为⑧的长方形周长是( )
A. 288 B. 178 C. 28 D. 110
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平面直角坐标系中,每个小正方形边长都是1.
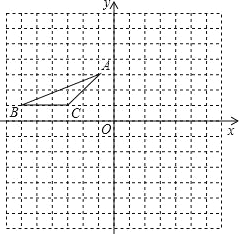
(1)按要求作图:
①△ABC关于x轴对称的图形△A1B1C1;
②将△A1B1C1向右平移7个单位得到△A2B2C2.
(2)回答下列问题:
①△A2B2C2中顶点B2坐标为 .
②若P(a,b)为△ABC边上一点,则按照(1)中①、②作图,点P对应的点P2的坐标为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 边长为
边长为![]() 的等边三角形
的等边三角形![]() 的顶点
的顶点![]() 分别在边
分别在边![]() ,
,![]() 上当
上当![]() 在边
在边![]() 上运动时,
上运动时,![]() 随之在边
随之在边![]() 上运动,等边三角形的形状保持不变,运动过程中,点
上运动,等边三角形的形状保持不变,运动过程中,点![]() 到点
到点![]() 的最大距离为( )
的最大距离为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(-2,0),B(0,6),C(6,0),∠ABC+∠ADC=180°,BC⊥CD.
(1)求证:∠ABO=∠CAD;
(2)求四边形ABCD的面积;
(3)如图2,E为∠BCO的邻补角的平分线上的一点,且∠BEO=45°,OE交BC于点F,求BF的长.

查看答案和解析>>
科目: 来源: 题型:
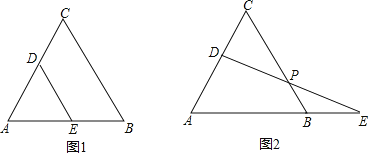
【题目】如图,D为等边△ABC的边AC上一点,E为直线AB上一点,CD=BE.
(1)如图1,求证;AD=DE;
(2)如图2,DE交CB于点P.
①若DE⊥AC,PC=6,求BP的长;
②猜想PD与PE之间的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com