
科目: 来源: 题型:
【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:

因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
查看答案和解析>>
科目: 来源: 题型:
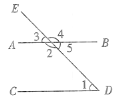
【题目】如图,直线AB,CD被DE所截,则∠1和 是同位角,∠1和 是内错角,∠1和 是同旁内角;
(2)在(1)中,如果∠5=∠1,那么∠1=∠3的推理过程如下,请在括号内注明理由:
因为∠5=∠1( ),
∠5=∠3( ),
所以∠1=∠3( ).
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴是x=﹣1,下列结论:(1)ac<0;(2)4ac<b2;(3)2a+b=0;(4)a﹣b+c>2,其中正确的结论共有( ) 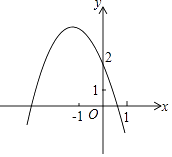
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则 ![]() 的长为( )
的长为( ) 
A.![]()
B.![]()
C.π
D.2π
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于点A(2,0)和点B,与y轴交于点C,顶点为点D,对称轴为直线x=﹣1,点E为线段AC的中点,点F为x轴上一动点.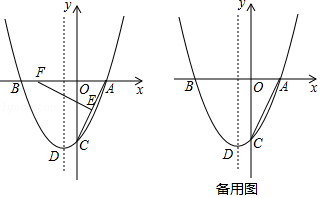
(1)直接写出点B的坐标,并求出抛物线的函数关系式;
(2)当点F的横坐标为﹣3时,线段EF上存在点H,使△CDH的周长最小,请求出点H,使△CDH的周长最小,请求出点H的坐标;
(3)在y轴左侧的抛物线上是否存在点P,使以P,F,C,D为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
科目: 来源: 题型:
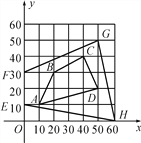
【题目】长阳公园有四棵古树A,B,C,D (单位:米).
(1)请写出A,B,C,D四点的坐标;
(2)为了更好地保护古树,公园决定将如图所示的四边形EFGH用围栏圈起来,划为保护区,请你计算保护区的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,一次函数![]() 的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
(1)直线CD的函数表达式为 ;(直接写出结果)
(2)点Q为线段DE上的一个动点,连接BQ.
①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标;
②将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上,请直接写出点Q的坐标: .

查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N.
(1)如图①,若△AMN是等边三角形,则∠BAC= °;
(2)如图②,若∠BAC=135°,求证:BM2+CN2=MN2.
(3)如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA的延长线于点H.若AB=4,CB=10,求AH的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com