
科目: 来源: 题型:
【题目】A厂一月份产值为16万元,因管理不善,二、三月份产值的月平均下降率为x(0<x<1).B厂一月份产值为12万元,二月份产值下降率为x,经过技术革新,三月份产值增长,增长率为2x.三月份A、B两厂产值分别为yA、yB(单位:万元).
(1)分别写出yA、yB与x的函数表达式;
(2)当yA=yB时,求x的值;
(3)当x为何值时,三月份A、B两厂产值的差距最大?最大值是多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④CF是AB的垂直平分线.以上结论正确的有( )个.
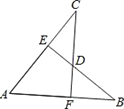
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
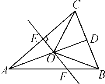
A. 3对 B. 4对 C. 5对 D. 6对
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目: 来源: 题型:
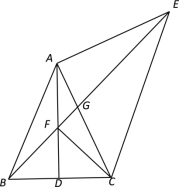
【题目】在△ABC中,AB=AC,∠BAC=50° ,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)求∠AEB的度数;
(2)求证:∠AEB=∠ACF;
(3)若AB=4,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:在△ABC中,∠C=30°,我们把∠A的对边与∠C 的对边的比叫做∠A的邻弦,记作thi A,即thi A= ![]() =
= ![]() .请解答下列问题: 已知:在△ABC中,∠C=30°.
.请解答下列问题: 已知:在△ABC中,∠C=30°.
(1)若∠A=45°,求thi A的值;
(2)若thi A= ![]() ,则∠A=°;
,则∠A=°;
(3)若∠A是锐角,探究thi A与sinA的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,∠B=45°, AM⊥BC,垂足为M.
(1)如图1,若AB=4![]() ,BC=7,求AC的长;
,BC=7,求AC的长;
(2)如图2, 点D是线段AM上一点,MD=MC,点E是△ABC外一点,CE=CA,连接ED并延长交BC于点F,且∠BDF=∠CEF,
求证①AC=BD;
②BF=CF.

查看答案和解析>>
科目: 来源: 题型:
【题目】同时点燃甲乙两根蜡烛,蜡烛燃烧剩下的长度y(cm)与燃烧时间x(min)的关系如图所示. 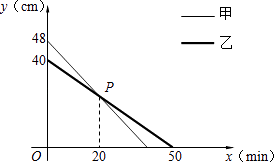
(1)求乙蜡烛剩下的长度y与燃烧时间x的函数表达式;
(2)求点P的坐标,并说明其实际意义;
(3)求点燃多长时间,甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车![]() 辆,B型车
辆,B型车![]() 辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】用两种方法证明“直角三角形斜边上的中线等于斜边的一半”.
已知:如图1,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD= ![]() AB.
AB.
证法1:如图2,在∠ACB的内部作∠BCE=∠B,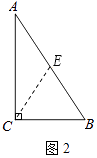
CE与AB相交于点E.
∵∠BCE=∠B,
∴ .
∵∠BCE+∠ACE=90°,
∴∠B+∠ACE=90°.
又∵ ,
∴∠ACE=∠A.
∴EA=EC.
∴EA=EB=EC,
即CE是斜边AB上的中线,且CE= ![]() AB.
AB.
又∵CD是斜边AB上的中线,即CD与CE重合,
∴CD= ![]() AB.
AB.
请把证法1补充完整,并用不同的方法完成证法2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com