
科目: 来源: 题型:
【题目】如图①,(1)已知∠ABC,射线ED∥AB,过点E作∠DEF=∠ABC,试说明BC∥EF;
(2)如图②,已知∠ABC,射线ED∥AB,∠ABC+∠DEF=180°.判断直线BC与直线EF的位置关系,并说明理由;
(3)根据以上探究,你发现了一个什么结论?请你写出来;
(4)如图③,已知AC⊥BC,CD⊥AB,DE⊥AC,HF⊥AB,若∠1=48°,试求∠2的度数.



查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度在直线AM上运动;已知AC=6cm,设动点D,E的运动时间为ts.
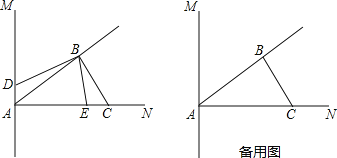
(1)试求∠ACB的度数;
(2)若![]() :
:![]() =2:3,试求动点D,E的运动时间t的值;
=2:3,试求动点D,E的运动时间t的值;
(3)试问当动点D,E在运动过程中,是否存在某个时间t,使得△ADB≌△CEB?若存在,请求出时间t的值;若不存在,请说出理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①所示,已知,BC∥OA,∠B=∠A=100°,试解答下列问题:
(1)试说明:OB∥AC;

(2)如图②,若点E.F在BC上,且∠FOC=∠AOC,OE平分∠BOF.试求∠EOC的度数;

(3)在(2)小题的条件下,若左右平行移动AC,如图③,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.

(4)在(3)小题的条件下,当∠OEB=∠OCA时,试求∠OCA的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,图①表示的是某教育网站一周内连续7天日访问总量的情况,图②表示的是学生日访问量占日访问总量的百分比情况,观察图①、②,解答下列问题:
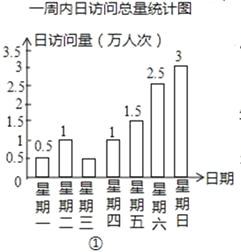
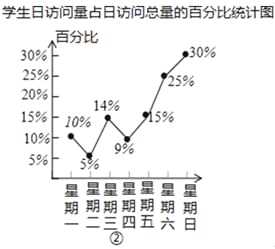
(1)若这7天的日访问总量一共约为10万人次,求星期三的日访问总量;
(2)求星期日学生日访问总量;
(3)请写出一条从统计图中得到的信息.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别(m) | 频数 |
1.09~1.19 | 8 |
1.19~1.29 | 12 |
1.29~1.39 | A |
1.39~1.49 | 10 |
(1)求a的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.

(1)求该一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).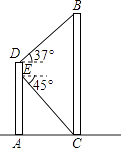
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解学生课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计。图(1)与图(2)是整理数据后绘制的两幅不完整的统计图。以下结论不正确的是( )
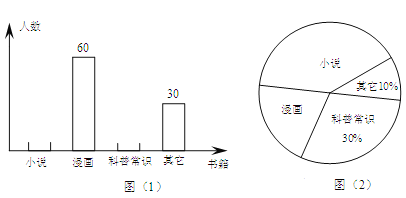
A. 由这两个统计图可知喜欢“科普常识”的学生有90人.
B. 若该年级共有1200名学生,则由这两个统计图可估计喜爱“科普常识”的学生约有360个.
C. 由这两个统计图不能确定喜欢“小说”的人数.
D. 在扇形统计图中,“漫画”所在扇形的圆心角为72°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com