【题目】下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A.
B.
C.
D.

【题目】如图所示，在Rt△ABC中，∠ACB=90，点D、F分别在AB、AC上，CF=CB，连接CD，将线段CD绕点按顺时针方向旋转90后得CE，连接EF．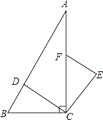
（1）求证：△BCD≌△FCE；
（2）若EF∥CD，求∠BDC的度数．

【题目】在平面直角坐标系中，为坐标原点，点的坐标为，点的坐标为，其中满足．

（1）若数没有平方根，判断点在第几象限并说明理由；

（2）若点到轴的距离是点到轴的距离的2倍，求点的坐标；

（3）若点的坐标为，三角形的面积是三角形面积的3倍，求点的坐标．

【题目】二次函数 的图象如图，给出下列四个结论：① ；② ；③ ；④ ，其中正确结论的个数是（ ）

A.4
B.3
C.2
D.1

【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AM、BN是△ABC的中线，AM⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．
（1）【特例探究】
如图1，当tan∠PAB=1，c=4 时，a= ， b=；
如图2，当∠PAB=30°，c=2时，a= ， b=；

（2）【归纳证明】
请你观察（1）中的计算结果，猜想a2、b2、c2三者之间的关系，用等式表示出来，并利用图3证明你的结论．

（3）【拓展证明】
如图4，ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=3 ，AB=3，求AF的长．

【题目】在平面直角坐标系中，对于任意三点的“矩面积”，给出如下定义：“水平底”是任意两点横坐标差的最大值；“铅垂高”是任意两点纵坐标差的最大值，则“矩面积”．例如：三点的坐标分别为，则“水平底”，“铅垂高”，“矩面积”．根据所给定义解决下面的问题：

（1）若点的坐标分别为，求这三点的“矩面积”；

（2）若点，含有的式子表示这三点的“矩面积”(结果需化简)；

（3）已知点，在轴上是否存在点，使这三点的“矩面积”为20？若存在，求出点的坐标；若不存在，请说明理由．

【题目】如图，在 中， ，以 的中点 为圆心分别与 ， 相切于 ， 两点，则 的长为（ ）
A.
B.
C.
D.

【题目】如图，抛物线y=ax2+bx+3交x轴于A（﹣1，0）和B（5，0），交y轴于点C，点D是线段OB上一动点，连接CD，将CD绕点D顺时针旋转90°得到线段DE，过点E作直线l⊥x轴，垂足为H，过点C作CF⊥l于F，连接DF，CE交于点G．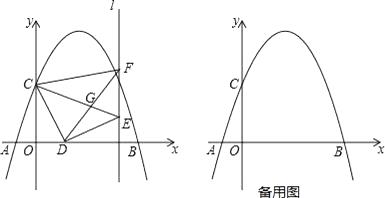

（1）求抛物线解析式；
（2）求线段DF的长；
（3）当DG= 时，
①求tan∠CGD的值；
②试探究在x轴上方的抛物线上，是否存在点P，使∠EDP=45°？若存在，请写出点P的坐标；若不存在，请说明理由．