
科目: 来源: 题型:
【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.

(1)补全△A′B′C′,利用网格点和直尺画图;
(2)图中AC与A1C1的关系是:______;
(3)画出△ABC中AB边上的中线CE;
(4)平移过程中,线段AC扫过的面积是_________
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,函数y=![]() 和y=﹣
和y=﹣![]() 的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为_______.
的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为_______.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠1+∠2=180°,∠3=∠B,试说明DE∥BC.下面是部分推导过程,请你在括号内填上推导依据或内容:
证明:∵∠1+∠2=180°(已知)
∠1=∠4 ( )
∴∠2+∠4=180°(等量代换)
∵EH∥AB( )
∴∠B= ( )
∵∠3=∠B(已知)
∴∠3=∠EHC(等量代换)
∴DE∥BC ( )

查看答案和解析>>
科目: 来源: 题型:
【题目】图①为平地上一幢建筑物与铁塔图,图②为其示意图.建筑物AB与铁塔CD都垂直于地面,BD=20m,在A点测得D点的俯角为45°,测得C点的仰角为58°.求铁塔CD的高度.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)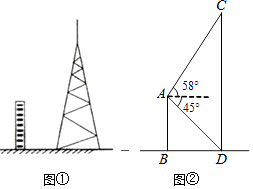
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:![]() 是
是![]() 的高,且
的高,且![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,点E在AD上,连接![]() ,将
,将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,若BE=BC,求
,若BE=BC,求![]() 的大小;
的大小;
(3)如图3,在(2)的条件下,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
图1.  图2.
图2.  图3.
图3. 
查看答案和解析>>
科目: 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1各单位,格点三角形(顶点是网格线的交点的三角形)△ABC的顶点A,B的坐标分别为(1,4),(﹣3,1).
(1)请在网格所在的平面内作出符合上述表述的平面直角坐标系;
(2)请你将A、B、C的横坐标不变,纵坐标乘以﹣1所得到的点A1、B1、C1描在坐标系中,并画出△A1B1C1,其中点C1的坐标为 .
(3)△ABC的面积是 .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1),在平面直角坐标系中,A(a,0),C(b,2),过C作CB⊥x轴,且满足(a+b)2+![]() =0.
=0.

(1)求三角形ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读以下材料:对数的创始人是苏格兰数学家纳皮尔(J.Napier,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到![]() 世纪瑞士数学家欧拉(L.Euler,1707-1783年)才发现指数与对数之间的联系.对数的定义:一般地,若
世纪瑞士数学家欧拉(L.Euler,1707-1783年)才发现指数与对数之间的联系.对数的定义:一般地,若![]() ,那么
,那么![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作:
的对数,记作:![]() .比如指数式
.比如指数式![]() 可以转化为
可以转化为![]() ,对数式
,对数式![]() 可以转化为
可以转化为![]() .我们根据对数的定义可得到对数的一个性质:
.我们根据对数的定义可得到对数的一个性质:![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() );理由如下:设
);理由如下:设![]() M=m,
M=m,![]() ,则
,则![]() ,
,![]()
![]() ,由对数的定义得
,由对数的定义得![]() 又
又![]() +
+![]()
![]() .解决一下问题:
.解决一下问题:
(1)将指数式![]() 转化为对数式___________;
转化为对数式___________;
(2)证明![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() );
);
(3)拓展运用:计算![]() =________.
=________.
查看答案和解析>>
科目: 来源: 题型:
【题目】细观察,找规律.
下列各图中的![]() 与
与![]() 平行.
平行.

![]() 图
图![]() 中的
中的![]() ______ 度,
______ 度,
图![]() 中的
中的![]() ______ 度,
______ 度,
图![]() 中的
中的![]() ______ 度,
______ 度,
图![]() 中的
中的![]() ______ 度,
______ 度,
![]() ,
,
第![]() 个图中的
个图中的![]() ______ 度
______ 度
![]() 第n个图中的
第n个图中的![]() ______
______
![]() 请你证明图
请你证明图![]() 的结论.
的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】市政府计划对城区道路进行改造,现安排甲、乙两个工程队共同完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造
倍,甲队改造![]() 米的道路比乙队改造同样长的道路少用
米的道路比乙队改造同样长的道路少用![]() 天.
天.
(1)甲、乙两个工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天的改造费用![]() 万元,乙队工作一天的改造费用为
万元,乙队工作一天的改造费用为![]() 万元,如需改造的道路全长为
万元,如需改造的道路全长为![]() 米,改造总费用不超过
米,改造总费用不超过![]() 万元,至少安排甲队工作多少天?
万元,至少安排甲队工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com