（1）作出△ABC绕点A顺时针方向旋转90°后得到的△A1B1C1，并写出C1点的坐标 ；

（2）作出△ABC关于原点O成中心对称的△A2B2C2，并求出△ABC的面积 ．

【题目】如图，在△ABC中，∠C=90°，AC=BC=，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接C′B，则C′B的长为( )．

A. 1 B. C. 2 D.

【题目】如图①，在矩形纸片ABCD中，AB= +1，AD= ．

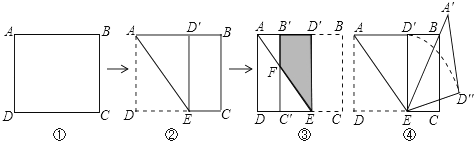
（1）如图②，将矩形纸片向上方翻折，使点D恰好落在AB边上的D′处，压平折痕交CD于点E，则折痕AE的长为 ．
（2）如图③，再将四边形BCED′沿D′E向左翻折，压平后得四边形B′C′ED′，B′C′交AE于点F，则四边形B′FED′的面积为 ．
（3）如图④，将图②中的△AED′绕点E顺时针旋转α角，得△A′ED″，使得EA′恰好经过顶点B，求弧D′D″的长 ． （结果保留π）

A. ①②④B. ③④⑤C. ①③④D. ①②⑤

（1）经过6秒后，BP=　　　　　　cm，BQ=　　　　　　cm；

（2）经过几秒后，△BPQ是直角三角形？

（3）经过几秒△BPQ的面积等于cm2？

(1)若p＝﹣4，q＝3，求方程x2+px+q＝0的两根．

(2)已知实数a、b满足a2﹣15a﹣5＝0，b2﹣15b﹣5＝0，求+的值；

(3)已知关于x的方程x2+mx+n＝0，(n≠0)，求出一个一元二次方程，使它的两个根分别是已知方程两根的倒数．

（1）若以每千克能盈利18元的单价出售,问每天的总毛利润为多少元?

（2）现市场要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每千克应涨价多少元?

（3）现需按毛利润的10%交纳各种税费,人工费每日按销售量每千克支出0．9元,水电房租费每日102元,若剩下的每天总纯利润要达到5100元,则每千克涨价应为多少?

【题目】如图，BE和CE分别为△ABC的内角平分线和外角平分线，BE⊥AC于点H，CF平分∠ACB交BE于点F连接AE．则下列结论：①∠ECF=90°；②AE=CE；③；④∠BAC=2∠BEC；⑤∠AEH=∠BCF，正确的个数为（ ）

A.2个B.3个C.4个D.5个

A. ∠BCA=∠F； B. ∠B=∠E； C. BC∥EF ； D. ∠A=∠EDF

【题目】如图，在正三角形ABC中，D，E，F分别是BC，AC，AB上的点，DE⊥AC，EF⊥AB，FD⊥BC，则△DEF的面积与△ABC的面积之比等于 ．