
【题目】如图①,在矩形纸片ABCD中,AB= ![]() +1,AD=
+1,AD= ![]() .
.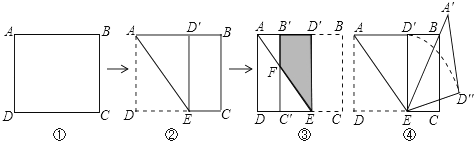
(1)如图②,将矩形纸片向上方翻折,使点D恰好落在AB边上的D′处,压平折痕交CD于点E,则折痕AE的长为 .
(2)如图③,再将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,B′C′交AE于点F,则四边形B′FED′的面积为 .
(3)如图④,将图②中的△AED′绕点E顺时针旋转α角,得△A′ED″,使得EA′恰好经过顶点B,求弧D′D″的长 . (结果保留π)
【答案】
(1)![]()
(2)![]() ﹣
﹣ ![]()
(3)![]()
【解析】解:(1)∵△ADE反折后与△AD′E重合,
∴AD′=AD=D′E=DE= ![]() ,
,
∴AE= ![]() =
= ![]() =
= ![]() ;
;
⑵∵由(1)知AD′= ![]() ,
,
∴BD′=1,
∵将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,
∴B′D′=BD′=1,
∵由(1)知AD′=AD=D′E=DE= ![]() ,
,
∴四边形ADED′是正方形,
∴B′F=AB′= ![]() ﹣1,
﹣1,
∴S梯形B′FED′= ![]() (B′F+D′E)B′D′=
(B′F+D′E)B′D′= ![]() (
( ![]() ﹣1+
﹣1+ ![]() )×1=
)×1= ![]() ﹣
﹣ ![]() ;
;
所以答案是:(1) ![]() ;(2)
;(2) ![]() ﹣
﹣ ![]() ;
;
⑶∵∠C=90°,BC= ![]() ,EC=1,
,EC=1,
∴tan∠BEC= ![]() =
= ![]() ,
,
∴∠BEC=60°,
由翻折可知:∠DEA=45°,
∴∠AEA′=75°=∠D′ED″,
∴ ![]() =
= ![]() .
.
【考点精析】利用勾股定理的概念和弧长计算公式对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
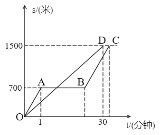
【题目】“龟兔赛跑”的故事同学们都听过,图中的线段OD和折线OABC表示龟兔赛跑时路程与时间的关系,请根据图中的信息,解决下列问题:
(1)填空:折线OABC表示赛跑过程中_________(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全程是_______米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来后以400米/分钟的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE和CE分别为△ABC的内角平分线和外角平分线,BE⊥AC于点H,CF平分∠ACB交BE于点F连接AE.则下列结论:①∠ECF=90°;②AE=CE;③![]() ;④∠BAC=2∠BEC;⑤∠AEH=∠BCF,正确的个数为( )
;④∠BAC=2∠BEC;⑤∠AEH=∠BCF,正确的个数为( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中,小格的顶点叫做格点。小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等。



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图 ![]() ,直线
,直线 ![]() 及直线
及直线 ![]() 外一点
外一点 ![]() .
.
求作:直线 ![]() ,使得
,使得 ![]() .
.
作法:如图 ![]() .
.
①在直线 ![]() 上取一点
上取一点 ![]() ,连接
,连接 ![]() ;
;
②作 ![]() 的平分线
的平分线 ![]() ;
;
③以点 ![]() 为圆心,
为圆心,![]() 长为半径画弧,交射线
长为半径画弧,交射线 ![]() 于点
于点 ![]() ;
;
④作直线 ![]() .
.
所以直线 ![]() 就是所求作的直线.根据小明设计的尺规作图过程.
就是所求作的直线.根据小明设计的尺规作图过程.
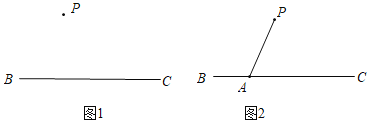
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:
![]() 平分
平分 ![]() ,
,
![]() .
.
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() (____________________)(填推理依据).
(____________________)(填推理依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中真命题的个数是( )
①平面内,过一点有且只有一条直线与已知直线平行;②![]() 这5个数中有2个是无理数;③若
这5个数中有2个是无理数;③若![]() ,则点P(-m,5)在第一象限;④
,则点P(-m,5)在第一象限;④![]() 的算术平方根是4;⑤经过一点有且只有一条直线与已知直线垂直;⑥同旁内角互补.
的算术平方根是4;⑤经过一点有且只有一条直线与已知直线垂直;⑥同旁内角互补.
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM;
(2)M为BC的中点.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com