【题目】已知，如图，线段AB，利用无刻度的直尺和圆规，作一个满足条件的△ABC：①△ABC为直角三角形；②tan∠A= ．（注：不要求写作法，但保留作图痕迹）

（1）实践：如图1， 中，为边上的中线，的面积记为，的面积记为．则．

（2）探究：在图2中，、分别为四边形的边、的中点，四边形的面积记为，阴影部分面积记为，则和之间满足的关系式为______：

（3）解决问题：

在图3中，、、、分别为任意四边形的边、、、的中点，并且图中阴影部分的面积为平方厘米，求图中四个小三角形的面积和，并说明理由．

（1）求证：四边形AECF是平行四边形；

（2）如果AE=3，EF=4，求AF、EC所在直线的距离．

一动点沿着数轴向右平移个单位，再向左平移个单位，相当于向右平移个单位．用有理数加法表示为．若坐标平面上的点做如下平移：沿轴方向平移的数量为（向右为正，向左为负，平移个单位），沿轴方向平移的数量为（向上为正，向下为负，平移个单位），则把有序数对叫做这一平移的“平移量”；“平移量”与“平移量”的加法运算法则为

解决问题：

（1）计算：；

（2）动点从坐标原点出发，先按照“平移量”平移到，再按照“平移量”平移到：若先把动点按照．“平移量”平移到，再按照“平移量”平移，最后的位置还是吗？在图1中画出四边形．

（3）如图2，一艘船从码头出发，先航行到湖心岛码头，再从码头航行到码头，最后回到出发点．请用“平移量”加法算式表示它的航行过程．

解：（1）______；

（2）答：______；

（3）加法算式：______．

【题目】如图，在平面直角坐标系中；长方形ABCD的四个顶点分别为；，，．对该长方形及其内部的每一个点都进行如下操作：把每个点的横坐标都乘以同一个实数，纵坐标都乘以3，再将得到的点向右平移个单位，向下平移个单位，得到长方形及其内部的点，其中点，，，的对应点分别为A’，B’，C’，D’，

（1）点A’的横坐标为______（用含，的式子表示）

（2）若点A’的坐标为，点C’的坐标为，求，的值．

(1)从这批衬衣众人抽1件是次品的概率约为多少？

(2)如果销售这批衬衣600件，那么至少要再准备多少件正品衬衣供买到次品的顾客更换？

（1）本次调查采用的调查方式是________（填“普查”或“抽样调查”），样本容量是________；

（2）补全频数分布直方图：

（3）若将月均用水量的频数绘成扇形统计图，则月均用水量“”的圆心角度数是________；

（4）若该小区有5000户家庭，求该小区月均用水量超过的家庭大约有多少户？

已知：AB∥CD∥EF，∠A＝110°，∠ACE＝100°，过点E作EH⊥EF,垂足为E，交CD于H点．

（1）依据题意，补全图形；

（2）求∠CEH的度数．

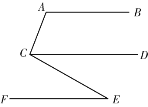
小明想了许久对于求∠CEH的度数没有思路，就去请教好朋友小丽，小丽给了他如图2所示的提示：

请问小丽的提示中理由①是 ；

提示中②是： 度；

提示中③是： 度；

提示中④是： ，理由⑤是 ．

提示中⑥是 度；

A. （m﹣n）°B. （90+n－m）°C. （90－n+m）°D. （180﹣2n﹣m）°