
科目: 来源: 题型:
【题目】在△ABC中,CA=CB,在△AED中,DA=DE,点D,E分别在CA,AB上.
(1)如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是;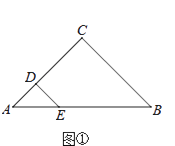
(2)若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,则CD与BE的数量关系是;,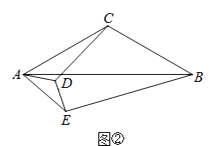
(3)若∠ACB=∠ADE=2α(0°<α<90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示).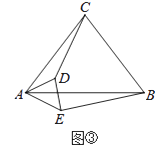
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=60°,OF⊥OE.
(1)判断OF把∠AOC所分成的两个角的大小关系并证明你的结论;
(2)求∠BOE的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=![]() x与直线l2交点A的横坐标为2,将直线l1沿y轴向下平移4个单位长度,得到直线l3,直线l3与y轴交于点B,与直线l2交于点C,点C的纵坐标为-2.直线l2与y轴交于点D.
x与直线l2交点A的横坐标为2,将直线l1沿y轴向下平移4个单位长度,得到直线l3,直线l3与y轴交于点B,与直线l2交于点C,点C的纵坐标为-2.直线l2与y轴交于点D.
(1)求直线l2的解析式;
(2)求△BDC的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】一辆出租车从超市(![]() 点)出发,向东走
点)出发,向东走![]() 到达小李家(
到达小李家(![]() 点),继续向东走
点),继续向东走![]() 到达小张家(
到达小张家(![]() 点),然后又回头向西走
点),然后又回头向西走![]() 到达小陈家(
到达小陈家(![]() 点),最后回到超市.
点),最后回到超市.
(1)以超市为原点,向东方向为正方向,用![]() 表示
表示![]() ,画出数轴,并在该数轴上表示
,画出数轴,并在该数轴上表示![]() 、
、![]() 、
、![]() 、
、![]() 的位置;
的位置;
(2)小陈家(![]() 点)距小李家(
点)距小李家(![]() 点)有多远?
点)有多远?
(3)若出租车收费标准如下,![]() 以内包括
以内包括![]() 收费
收费![]() 元,超过
元,超过![]() 部分按每千米
部分按每千米![]() 元收费,则从超市出发到回到超市一共花费多少元?
元收费,则从超市出发到回到超市一共花费多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】白色污染( Whitepollution)是人们对难降解的塑料垃圾(多指塑料袋)污染环境现象的一种形象称谓.为了让全校同学感受丢弃塑料袋对环境的影响,小彬随机抽取某小区![]() 户居民,记录了这些家庭
户居民,记录了这些家庭![]() 年某个月丢弃塑料袋的数量(单位:个)
年某个月丢弃塑料袋的数量(单位:个)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请根据上述数据,解答以下问题:

(1)小彬按“组距为![]() ”列出了如下的频数分布表(每组数据含最小值不含最大值),请将表中空缺的部分补充完整,并补全频数直方图;
”列出了如下的频数分布表(每组数据含最小值不含最大值),请将表中空缺的部分补充完整,并补全频数直方图;
分组 | 划记 | 频数 |
| _______ | ________ |
|
|
|
| _______ | ________ |
|
|
|
合计 | / |
|
(2)根据(1)中的直方图可以看出,这![]() 户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
(3)根据频数分布表,小彬又画出了如图所示的扇形统计图.请将统计图中各组占总数的百分比填在图中,并求出![]() 组对应的扇形圆心角的度数;
组对应的扇形圆心角的度数;
(4)若该小区共有![]() 户居民家庭,请你估计每月丢弃的塑料袋数量不小于
户居民家庭,请你估计每月丢弃的塑料袋数量不小于![]() 个的家庭个数.
个的家庭个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】2015年某企业按餐厨垃圾处理费50元/吨、建筑垃圾处理费20元/吨的收费标准,共支付餐厨和建筑垃圾处理费7000元.从2016年元月起,收费标准上调为:餐厨垃圾处理费120元/吨,建筑垃圾处理费40元/吨.若该企业2016年处理的这两种垃圾数量与2015年相比没有变化,就要多支付垃圾处理费8600元.
(1)该企业2015年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2016年将上述两种垃圾处理总量减少到200吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2016年该企业最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】从甲、乙两名射击选手中选出一名选手参加省级比赛,现对他们分别进行5次射击测试,成绩分别为(单位:环)甲:5、6、7、9、8;乙:8、4、8、6、9,
(1)甲运动员5次射击成绩的中位数为________环,极差是________环;乙运动员射击成绩的众数为________环.
(2)已知甲的5次成绩的方差为2,通过计算,判断甲、乙两名运动员谁的成绩更稳定.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),反比例函数的图象经过点C.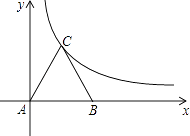
(1)求点C的坐标及反比例函数的解析式.
(2)将等边△ABC向上平移n个单位,使点B恰好落在双曲线上,求n的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A的坐标为(-4,4),点B的坐标为(0,2).

(1)求直线AB的解析式;
(2)以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴于点C,射线AD交y轴的负半轴于点D.当∠CAD绕着点A旋转时,OC-OD的值是否发生变化?若不变,求出它的值;若变化,求出它的变化范围;
(3)如图2,点M(-4,0)和N(2,0)是x轴上的两个点,点P是直线AB上一点.当△PMN是直角三角形时,请求出满足条件的所有点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】保障房建设是民心工程,某市从2012年开始加快保障房建设进程,现统计了该市2012年到2016年5月新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.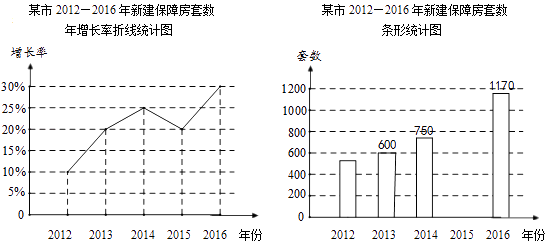
(1)小丽看了统计图后说:“该市2015年新建保障房的套数比2014年少了.”你认为小丽说法正确吗?请说明理由;
(2)求补全条形统计图;
(3)求这5年平均每年新建保障房的套数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com