
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).
其中正确的结论有( )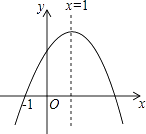
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目: 来源: 题型:
【题目】在正方形ABCD中,连接BD.
(1)如图1,AE⊥BD于E.直接写出∠BAE的度数.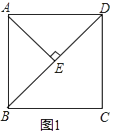
(2)如图1,在(1)的条件下,将△AEB以A旋转中心,沿逆时针方向旋转30°后得到△AB′E′,AB′与BD交于M,AE′的延长线与BD交于N.
①依题意补全图1;
②用等式表示线段BM、DN和MN之间的数量关系,并证明.
(3)如图2,E、F是边BC、CD上的点,△CEF周长是正方形ABCD周长的一半,AE、AF分别与BD交于M、N,写出判断线段BM、DN、MN之间数量关系的思路.(不必写出完整推理过程)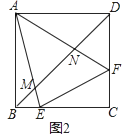
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A. (2,5)B. (5,2)C. (2,﹣5)D. (5,﹣2)
查看答案和解析>>
科目: 来源: 题型:
【题目】收集和整理数据.
某中学七(1)班学习了统计知识后,数学老师要求每个学生就本班学生的上学方式进行一次全面调查,如图是一同学通过收集数据后绘制的两幅不完整的统计图,请根据图中提供的信息,解答下列问题:(每个学生只选择1种上学方式).

(1)求该班乘车上学的人数;
(2)将频数分布直方图补充完整;
(3)若该校七年级有1200名学生,能否由此估计出该校七年级学生骑自行车上学的人数,为什么?
查看答案和解析>>
科目: 来源: 题型:
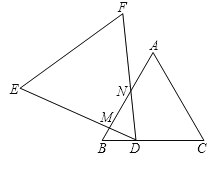
【题目】将两个等边△ABC和△DEF(DE>AB)如图所示摆放,点D是BC上的一点(除B、C点外).把△DEF绕顶点D顺时针旋转一定的角度,使得边DE、DF与△ABC的边(除BC边外)分别相交于点M、N.
(1)∠BMD和∠CDN相等吗?
(2)画出使∠BMD和∠CDN相等的所有情况的图形.
(3)在(2)题中任选一种图形说明∠BMD和∠CDN相等的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间关系的图像如图所示.根据图像解答下列问题:
(1)谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2)分别求出甲、乙两人的行驶速度;
(3)在什么时间段内,两人均行驶在途中?(不包括起点和终点)

查看答案和解析>>
科目: 来源: 题型:
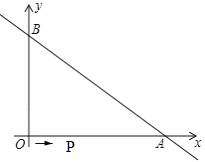
【题目】如图,直线![]() 与坐标轴分别交于A、B两点,OA=8,OB=6.动点P从O点出发,沿路线O→A→B以每秒2个单位长度的速度运动,到达B点时运动停止.
与坐标轴分别交于A、B两点,OA=8,OB=6.动点P从O点出发,沿路线O→A→B以每秒2个单位长度的速度运动,到达B点时运动停止.
(1)则A点的坐标为_____,B两点的坐标为______;
(2)当点P在OA上,且BP平分∠OBA时,则此时点P的坐标为______;
(3)设点P的运动时间为t秒(0≤t≤4),△BPA的面积为S,求S与t之间的函数关系式:并直接写出当S=8时点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
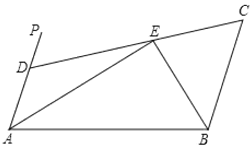
【题目】如图,![]() ,
,![]() PAB的平分线与
PAB的平分线与![]() CBA的平分线相交于E,CE的延长线交AP于D,求证:
CBA的平分线相交于E,CE的延长线交AP于D,求证:
(1)AB=AD+BC;
(2)若BE=3,AE=4,求四边形ABCD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,直线AC∥BD,连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA、PB,构成∠PAC、∠APB、∠PBD三个角(提示:有公共端点的两条重合的射线所组成的角是0°).
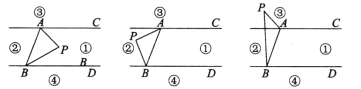
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD.
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立(直接回答成立或不成立);
(3)当动点P在第③部分时,全面探究∠PAC、∠APB、∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com