
科目: 来源: 题型:
【题目】防疫期间的某天上午9:00,社区工作人员小孙从社区办公室出发,上门为本社区两户隔离人员家庭送生活用品,同时了解隔离人员的健康状况,她先去了距离社区较近的张家,稍作停留简单询问了情况后,又去了稍远一点的李家,这家人口较多,了解情况时间稍长一些,由于社区还有其它事情等待处理,结束工作后她快速返回社区办公室.已知小孙距离社区办公室的距离![]() (米)与离开办公室的时间
(米)与离开办公室的时间![]() (分)之间的关系如图所示.请根据图象回答下列问题:
(分)之间的关系如图所示.请根据图象回答下列问题:

(1)图中![]() 点表示的意义是什么?
点表示的意义是什么?
(2)小孙从李家出来后步行的速度是多少?
(3)小孙在李家停留了几分钟?小孙几点回到社区办公室?
查看答案和解析>>
科目: 来源: 题型:
【题目】问题提出:
![]() ,
,![]() 分别是什么数时,多项式
分别是什么数时,多项式![]() 和
和![]() 恒等?
恒等?
阅读理解:
所谓恒等式,就是指不论用任何数值来代替式中的变量,左、右两边的值都相等的等式.我们用符号“![]() ”来表示恒等,读作“恒等于”.于是,上面的问题也可以表述为:已知
”来表示恒等,读作“恒等于”.于是,上面的问题也可以表述为:已知![]() ,求待定系数
,求待定系数![]() ,
,![]() .
.
问题解决:
(方法1—数值代入法)由恒等式的概念,我们每用一个数值来代替问题中的![]() ,即可得到一个关于
,即可得到一个关于![]() 与
与![]() 的方程.因此,要求出
的方程.因此,要求出![]() 与
与![]() 的值,只需要用两个不同的数值分别代替式中的
的值,只需要用两个不同的数值分别代替式中的![]() ,就可以得到一个关于
,就可以得到一个关于![]() 与
与![]() 的二元一次方程组,解这个方程组,即可求得
的二元一次方程组,解这个方程组,即可求得![]() 与
与![]() .
.
解:分别用![]() ,
,![]() 代替式中的
代替式中的![]() ,得
,得
![]()
解之,得![]()
(方法2—系数比较法)
定理 如果![]() ,
,
那么![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据这个定理,也可以这样解:
解:由题设![]() ,
,
比较对应项的系数,得![]() ,
,![]() .
.
请回答下面的问题:
(1)已知多项式![]() .求
.求![]() 与
与![]() 的值;
的值;
(2)如果![]() 被
被![]() 除后余
除后余![]() ,求
,求![]() 的值及商式.
的值及商式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,AD=8,点E在BC边上,且BE:EC=1:3.动点P从点B出发,沿BA运动到点A停止.过点E作EF⊥PE交边AD或CD于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为__________.

查看答案和解析>>
科目: 来源: 题型:
【题目】为了保护环境,某化工厂一期工程完成后购买了![]() 台甲型和
台甲型和![]() 台乙型污水处理设备,共花费资金
台乙型污水处理设备,共花费资金![]() 万元,且每台乙型设备的价格是每台甲型设备价格的
万元,且每台乙型设备的价格是每台甲型设备价格的![]() ,实际运行中发现,每台甲型设备每月能处理污水
,实际运行中发现,每台甲型设备每月能处理污水![]() 吨,每台乙型设备每月能处理污水
吨,每台乙型设备每月能处理污水![]() 吨.今年该厂二期工程即将完成产生的污水将大大增加,于是该厂决定再购买甲、乙两种型号设备共
吨.今年该厂二期工程即将完成产生的污水将大大增加,于是该厂决定再购买甲、乙两种型号设备共![]() 台用于二期工程的污水处理,预算本次购买资金不超过
台用于二期工程的污水处理,预算本次购买资金不超过![]() 万元,预计二期工程完成后每月将产生不少于
万元,预计二期工程完成后每月将产生不少于![]() 吨污水.
吨污水.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少元;
(2)请你求出用于二期工程的污水处理设备的所有购买方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了![]() (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应![]() 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着![]() 展开式中的系数等等.
展开式中的系数等等.

(1)根据上面的规律,写出![]() 的展开式.
的展开式.
(2)利用上面的规律计算:![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】类比特殊四边形的学习,我们可以定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)【探索体验】如图1,已知在四边形ABCD中,∠A=40°,∠B=100°,∠C=120°.求证:四边形ABCD是“等对角四边形”.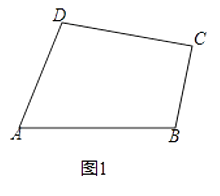
(2)如图2,若AB=AD=a,CB=CD=b,且a≠b,那么四边形ABCD是“等对角四边形”吗?试说明理由.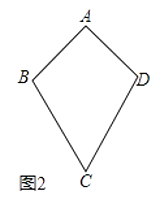
(3)【尝试应用】如图3,在边长为6的正方形木板ABEF上裁出“等对角四边形”ABCD,若已经确定DA=4m,∠DAB=60°,是否在正方形ABEF内(包括边上)存在一点C,使四边形ABCD以∠DAB=∠BCD为等对角的四边形的面积最大?若存在,试求出四边形ABCD的最大面积;若不存在,请说明理由.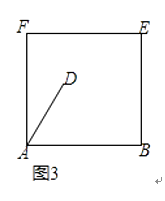
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线C1:y=ax2+bx+4与x轴交于A(﹣3,0),B两点,与y轴交于点C,点M(﹣ ![]() ,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.
,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.
(1)求抛物线C1的解析式;
(2)过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() .
.



(1)如图1,直接写出![]() ,
,![]() 和
和![]() 之间的数量关系.
之间的数量关系.
(2)如图2,![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,那么
,那么![]() 和
和![]() 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.
(3)若点E的位置如图3所示,![]() ,
,![]() 仍分别平分
仍分别平分![]() ,
,![]() ,请直接写出
,请直接写出![]() 和
和![]() 的数量关系.
的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com