
科目: 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
根据以上信息,解答下列问题:
(1)设租车时间为 ![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 ![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 ![]() 元,分别求出
元,分别求出 ![]() ,
, ![]() 关于
关于 ![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:
在平面直角坐标系xOy中,点P(x0 , y0)到直线Ax+By+C=0的距离公式为:d= ![]() .
.
例如:求点P0(0,0)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知,A=4,B=3,C=﹣3,
∴点P0(0,0)到直线4x+3y﹣3=0的距离为d= ![]() =
= ![]() .
.
根据以上材料,解决下列问题:
(1)点P1(3,4)到直线y=﹣ ![]() x+
x+ ![]() 的距离为;
的距离为;
(2)已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线y=﹣ ![]() x+b相切,求实数b的值;
x+b相切,求实数b的值;
(3)如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出S△ABP的最大值和最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
查看答案和解析>>
科目: 来源: 题型:
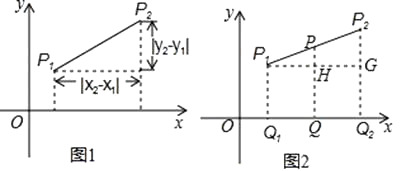
【题目】小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1 , y1),P2(x2 , y2),可通过构造直角三角形利用图1得到结论:P1P2= ![]() 他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x=
他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x= ![]() ,y=
,y= ![]() .
.
(1)请你帮小明写出中点坐标公式的证明过程;
(2)①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;
②直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标:;
(3)如图3,点P(2,n)在函数y= ![]() x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.
x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.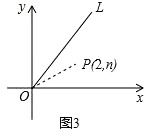
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.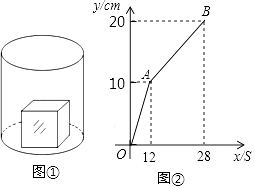
(1)正方体的棱长为cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com