
科目: 来源: 题型:
【题目】已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD,
(1)求证:DF与⊙O的位置关系并证明;
(2)求FG的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形 ABEF 的面积为 4,△BCE 是等边三角形,点 C 在正方形ABEF 外,在对角线 BF 上有一点 P,使 PC+PE 最小,则这个最小值的平方为( )
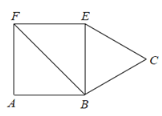
A.![]() B.
B.![]() C.12D.
C.12D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|2a﹣b+8|+(a+b﹣2)2=0.

(1)求a、b的值;
(2)如图1,点G在y轴上,三角形COG的面积是三角形ABC的面积的![]() ,求出点G的坐标;
,求出点G的坐标;
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一个动点,连接OP、AC、DB,OE平分∠AOP,OF⊥CE,若∠OPD+k∠DOF=k(∠FOP+∠AOE),现将四边形ABDC向下平移![]() k个单位得到四边形A1B1D1C1,已知AM+BN =
k个单位得到四边形A1B1D1C1,已知AM+BN =![]() k,求图中阴影部分的面积.
k,求图中阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 坐标为
坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数的解析式和一次函数的解析式;
(2)连结![]() ,求
,求![]() 的面积;
的面积;
(3)观察图象直接写出![]() 时
时![]() 的取值范围是 ;
的取值范围是 ;
(4)直接写出:![]() 为
为![]() 轴上一动点,当三角形
轴上一动点,当三角形![]() 为等腰三角形时点
为等腰三角形时点![]() 的坐标 .
的坐标 .


查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).
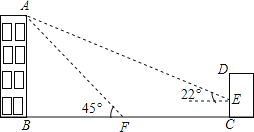
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】参照学习函数的过程与方法,探究函数![]() 的图象与性质.
的图象与性质.
因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究.
来探究.
列表:
| … |
|
|
|
|
|
| 1 | 2 | 3 | 4 | … |
| … |
|
| 1 | 2 | 4 |
|
| 1 |
|
| … |
| … |
|
| 2 | 3 | 5 |
|
| 0 |
|
| … |
描点:在平面直角坐标系中,以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出了相应的点(如图所示).
相应的函数值为纵坐标,描出了相应的点(如图所示).
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而 ;(填“增大”或“减小”)
的增大而 ;(填“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;
③![]() 图象关于点 成中心对称.(填点的坐标)
图象关于点 成中心对称.(填点的坐标)

查看答案和解析>>
科目: 来源: 题型:
【题目】某校九年级组织有奖知识竞赛,派小明去购买A、B两种品牌的钢笔作为奖品.已知一支A品牌钢笔的价格比一支B品牌钢笔的价格多5元,且买100元A品牌钢笔与买50元B品牌钢笔数目相同.
(1)求A、B两种品牌钢笔的单价分别为多少元?
(2)根据活动的设奖情况,决定购买A、B两种品牌的钢笔共100支,如果设购买A品牌钢笔的数量为n支,购买这两种品牌的钢笔共花费y元.
①直接写出y(元)关于n(支)的函数关系式;
②如果所购买A品牌钢笔的数量不少于B品牌钢笔数量的![]() ,请你帮助小明计算如何购买,才能使所花费的钱最少?此时花费是多少?
,请你帮助小明计算如何购买,才能使所花费的钱最少?此时花费是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】操作发现:
(1)如图,在平面直角坐标系中有一点![]() ,将点
,将点![]() 先向右平移3个单位长度,再向下平移3个单位长度得到点
先向右平移3个单位长度,再向下平移3个单位长度得到点![]() ,则点
,则点![]() 的坐标为 ;并在图中画出直线
的坐标为 ;并在图中画出直线![]() 的函数图象;
的函数图象;
(2)直接写出直线![]() 的解析式 ;
的解析式 ;
(3)若直线![]() 上有一动点
上有一动点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①直接写出点![]() 的坐标 ;
的坐标 ;
②若点![]() 位于第四象限,直接写出三角形
位于第四象限,直接写出三角形![]() 的面积 .(用含
的面积 .(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如下:
频率分布统计表 | 频率分布直方图 | ||
分数段 | 频数 | 频率 |
|
60≤x<70 | 40 | 0.40 | |
70≤x<80 | 35 | b | |
80≤x<90 | a | 0.15 | |
90≤x<100 | 10 | 0.10 | |
请根据上述信息,解答下列问题:
(1)表中:a= ,b= ;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.
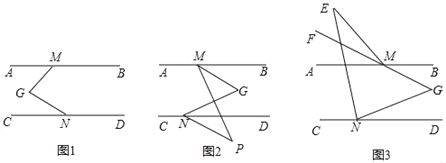
(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;
(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG=30°,求∠MGN+∠MPN的度数;
(3)如图3,若点E是AB上方一点,连接EM、EN,且GM的延长线MF平分∠AME,NE平分∠CNG,2∠MEN+∠MGN=105°,求∠AME的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com