
科目: 来源: 题型:
【题目】二次函数![]() 的图像交y轴于C点,交
的图像交y轴于C点,交![]() 轴于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程![]() 的两个根.
的两个根.
(1)求出点A、点B的坐标及该二次函数表达式.

(2)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合),过点Q作QD∥AC交于BC点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.
(3)如图3,线段MN是直线y=x上的动线段(点M在点N左侧),且MN=![]() ,若M点的横坐标为n,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出n的值;若不能,请说明理由.
,若M点的横坐标为n,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出n的值;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
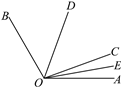
【题目】已知∠AOC和∠BOC,OD平分∠BOC,OE平分∠AOC.
(1)请写出一对相等的角;
(2)若∠AOC在∠BOC的外部,且∠AOB=120°,如图,其他条件不变,求∠EOD的度数.从结果你能看出∠EOD与∠AOB有什么数量关系吗?
(3)若∠AOC=α,∠BOC=β(α,β都大于0°且小于180°,且α<β),其他条件不变,试求∠EOD的度数(结果用含α,β的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
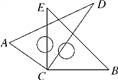
【题目】如图,将两块直角三角尺的顶点叠放在一起.
(1)若∠DCE=35°,求∠ACB的度数;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB与∠DCE的关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
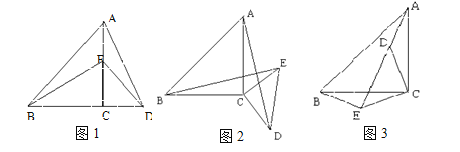
【题目】如图1,E是等腰Rt△ABC边AC上的一个动点(点E与A、C不重合),以CE为一边在Rt△ABC作等腰Rt△CDE,连结AD,BE.我们探究下列图中线段AD,、线段BE 的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;
②将图1中的等腰Rt△CDE绕着点C按顺时针方向旋转任意角度![]() ,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
(2)将原题中等腰直角三角形改为直角三角形(如图4—6),且AC=a,BC=b,CD=ka,CE=kb (a![]() b,k
b,k![]() 0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
(3)在第(2)题图5中,连结BD、AE,且a=4,b=3,k=![]() ,求BD2+AE2的值.
,求BD2+AE2的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公园的门票每张20元,一次性使用.考虑到人们的不同需求,也为了吸引更多的游客,该公园除保留原来的售票方法外,还推出了一种“购买个人年票”(个人年票从购买日起,可供持票者使用一年)的售票方法.年票分A,B,C三类,A类年票每张240元,持票进入该园区时,无需再购买门票;B类年票每张120元,持票者进入该园区时,需再购买门票,每次4元;C类年票每张80元,持票者进入该园区时,需再购买门票,每次6元.
(1)如果只能选择一种购买年票的方式,并且计划在一年中花费160元在该公园的门票上,通过计算,找出可进入该园区次数最多的方式.
(2)一年中进入该公园超过多少次时,A类年票比较合算?
查看答案和解析>>
科目: 来源: 题型:
【题目】我市某工艺厂为迎“五一”,设计了一款成本为20元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
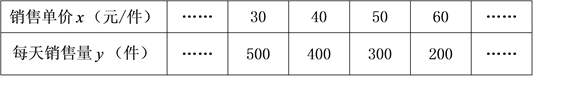
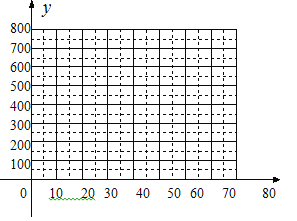
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
查看答案和解析>>
科目: 来源: 题型:
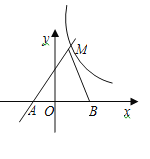
【题目】如图,直线y=kx+k(k≠0)与双曲线![]() 在第一象限内相交于点M,与x轴交于点A.
在第一象限内相交于点M,与x轴交于点A.
(1)求m的取值范围和点A的坐标;
(2)若点B的坐标为(3,0),AM=5,S△ABM=8,求双曲线的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
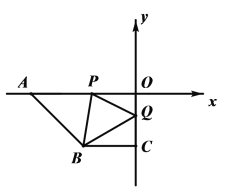
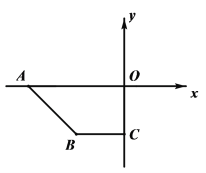
【题目】如图,在平面直角坐标系xOy中,点A(a,0),B(c,c),C(0,c),且满足![]() ,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.
,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.
(1)直接写出点B的坐标,AO和BC位置关系是;
(2)当P、Q分别是线段AO,OC上时,连接PB,QB,使![]() ,求出点P的坐标;
,求出点P的坐标;
(3)在P、Q的运动过程中,当∠CBQ=30°时,请探究∠OPQ和∠PQB的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com