
科目: 来源: 题型:
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )
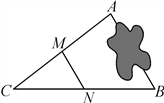
A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图, ![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 延长线上任意一点,以
延长线上任意一点,以![]() 为直角边作等腰直角
为直角边作等腰直角![]() ,且
,且![]() ,连结
,连结![]() .
.
(![]() )求证:
)求证: ![]() .
.
(![]() )在点
)在点![]() 运动过程中,试问
运动过程中,试问![]() 的度数是否会变化?若不变,请求出它的度数,若变化,请说明它的变化趋势.
的度数是否会变化?若不变,请求出它的度数,若变化,请说明它的变化趋势.
(![]() )已知
)已知![]() ,设
,设![]() ,
, ![]() .
.
①试求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
②当![]() 时,求
时,求![]() 的外接圆半径.
的外接圆半径.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第100个图中正方形和等边三角形的个数之和是( )

A. 900 B. 903 C. 906 D. 807
查看答案和解析>>
科目: 来源: 题型:
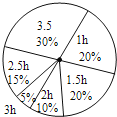
【题目】初三年级学习压力大,放学后在家自学时间较初一、初二长,为了解学生学习时间,该年级随机抽取25%的学生问卷调查,制成统计表和扇形统计图,请你根据图表中提供的信息回答下列问题:
学习时间(h) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
人数 | 72 | 36 | 54 | 18 |
(1)初三年级共有学生_____人.
(2)在表格中的空格处填上相应的数字.
(3)表格中所提供的学生学习时间的中位数是_____,众数是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;
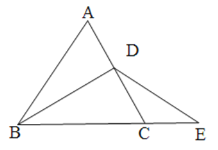
图1
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立,请说明理由.
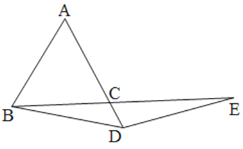
图2
查看答案和解析>>
科目: 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)当x>1时,请分別直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)在(1)的条件下,小明选择哪家快递公司更省钱?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(![]() )
)![]() 分别取
分别取![]() ,
, ![]() ,
, ![]() 时,试求出各函数表达式,并说出这三个函数的一个共同点.
时,试求出各函数表达式,并说出这三个函数的一个共同点.
(![]() )对于任意负实数
)对于任意负实数![]() ,当
,当![]() 时,
时, ![]() 随
随![]() 的增大而增大,试求出
的增大而增大,试求出![]() 的最大整数值.
的最大整数值.
(![]() )点
)点![]() ,
, ![]() 是函数图象上两个点,满足若
是函数图象上两个点,满足若![]() ,试比较
,试比较![]() 和
和![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目: 来源: 题型:
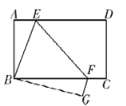
【题目】如图,矩形![]() 边
边![]() ,
,![]() ,沿
,沿![]() 折叠,使
折叠,使![]() 点与
点与![]() 点重合,
点重合,![]() 点的对应点为
点的对应点为![]() ,将
,将![]() 绕着点
绕着点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]()
![]() .记旋转过程中的三角形为
.记旋转过程中的三角形为![]() ,在旋转过程中设直线
,在旋转过程中设直线![]() 与射线
与射线![]() 、射线
、射线![]() 分别交于点
分别交于点![]() 、
、![]() ,当
,当![]() 时,则
时,则![]() 的长为_______.
的长为_______.
查看答案和解析>>
科目: 来源: 题型:
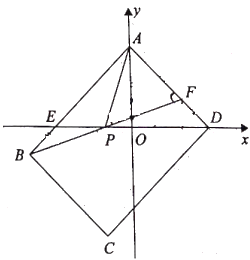
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 在坐标轴上,两点的坐标分别是点
在坐标轴上,两点的坐标分别是点![]() 点
点![]() 且
且![]() 满足:
满足:![]()
![]() 边
边![]() 与
与![]() 轴交于点
轴交于点![]() 点
点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,分别与
,分别与![]() 轴,
轴,![]() 轴交于点
轴交于点![]() 点
点![]() 且
且![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 求证:
求证:![]() ;
;
(3)若点![]() 的纵坐标为
的纵坐标为![]() 则线段HF的长为 .(用含
则线段HF的长为 .(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com