
科目: 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】在将式子![]() (m>0)化简时,
(m>0)化简时,
小明的方法是:![]() =
=![]() =
=![]() =
=![]() ;
;
小亮的方法是: ![]() ;
;
小丽的方法是:![]() .
.
则下列说法正确的是( )
A. 小明、小亮的方法正确,小丽的方法不正确
B. 小明、小丽的方法正确,小亮的方法不正确
C. 小明、小亮、小丽的方法都正确
D. 小明、小丽、小亮的方法都不正确
查看答案和解析>>
科目: 来源: 题型:
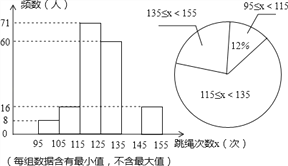
【题目】在我市开展的“阳光体育”跳绳活动中,为了了解中学生跳绳活动的开展情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制两个不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图空缺部分,直接写出扇形统计图中跳绳次数范围135≤x≤155所在扇形的圆心角度数.
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).

解:∵∠BAE+∠AED=180°(已知)
∴ ∥ (同旁内角互补,两直线平行)
∴∠BAE= (两直线平行,内错角相等)
又∵∠1=∠2
∴∠BAE﹣∠1= ﹣
即∠MAE=
∴ ∥ (内错角相等,两直线平行)
∴∠M=∠N(两直线平行,内错角相等)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点A,B,C的坐标分别为(a,0),(2,﹣4),(c,0),且a,c满足方程![]() 为二元一次方程.
为二元一次方程.
(1)求A,C的坐标.
(2)若点D为y轴正半轴上的一个动点.
①如图1,∠AOD+∠ADO+∠DAO=180°,当AD∥BC时,∠ADO与∠ACB的平分线交于点P,求∠P的度数;
②如图2,连接BD,交x轴于点E.若S△ADE≤S△BCE成立.设动点D的坐标为(0,d),求d的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )

A.四边形AEDF是平行四边形
B.若∠BAC=90°,则四边形AEDF是矩形
C.若AD平分∠BAC,则四边形AEDF是矩形
D.若AD⊥BC且AB=AC,则四边形AEDF是菱形
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知菱形![]() 的边长为6,
的边长为6,![]() , 点
, 点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的动点(不与端点重合),且
上的动点(不与端点重合),且![]() .
.
(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)点![]() 、
、![]() 在运动过程中,四边形
在运动过程中,四边形![]() 的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
(3)当点![]() 在什么位置时,
在什么位置时,![]() 的面积最大,并求出此时面积的最大值;
的面积最大,并求出此时面积的最大值;
(4)如图2,连接![]() 分别与边
分别与边![]() 、
、![]() 交于
交于![]() 、
、![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】进入六月以来,西瓜出现热卖.佳佳水果超市用760元购进甲、乙两个品种的西瓜,销售完共获利360元,其进价和售价如表:
甲品种 | 乙品种 | |
进价(元/千克) | 1.6 | 1.4 |
售价(元/千克) | 2.4 | 2 |
(1)求佳佳水果超市购进甲、乙两个品种的西瓜各多少千克?
(2)由于销售较好,该超市决定,按进价再购进甲,乙两个品种西瓜,购进乙品种西瓜的重量不变,购进甲品种西瓜的重量是原来的2倍,甲品种西瓜按原价销售,乙品种西瓜让利销售.若两个品种的西瓜售完获利不少于560元,问乙品种西瓜最低售价为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,AB∥CD,E是射线FD上的一点,∠ABC=140°,∠CDF=40°
(1)试说明BC∥EF;
(2)若∠BAE=110°,连接BD,如图2.若BD∥AE,则BD是否平分∠ABC,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,反比例函数![]() 与一次函数
与一次函数![]() 的图像交于点
的图像交于点![]() ,
,![]() .
.

(1)求![]() ,
,![]() 的值;
的值;
(2)结合函数图像,写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)![]() 为
为![]() 轴上一点,若
轴上一点,若![]() 的面积是
的面积是![]() 面积的3倍,请求出点
面积的3倍,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com