
【题目】如图1,已知菱形![]() 的边长为6,
的边长为6,![]() , 点
, 点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的动点(不与端点重合),且
上的动点(不与端点重合),且![]() .
.
(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)点![]() 、
、![]() 在运动过程中,四边形
在运动过程中,四边形![]() 的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
(3)当点![]() 在什么位置时,
在什么位置时,![]() 的面积最大,并求出此时面积的最大值;
的面积最大,并求出此时面积的最大值;
(4)如图2,连接![]() 分别与边
分别与边![]() 、
、![]() 交于
交于![]() 、
、![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.

【答案】(1)见解析;(2)四边形AECF的面积不变.四边形AECF的面积为![]() ;(3)E是BC的中点时△ECF的面积最大,最大面积为
;(3)E是BC的中点时△ECF的面积最大,最大面积为![]() ;(4)见解析
;(4)见解析
【解析】
(1)利用证明△ACE和△ADF全等得AE=AF,结合∠EAF=60°,便得△EAF是等边三角形;
(2)根据△ACE≌△ADF,得四边形AECF的面积等于△ACD的面积等于菱形ABCD面积的一半;
(3)要使三角形ECF的面积最大,只要等边三角形AEF的面积最小即AE⊥BC时即可;
(4)将△ADN绕点A顺时针旋转120°得到△ABP,连接PM.证明MN=PM,∠BPM=90°即可解决问题.
(1)证明:在菱形ABCD中,
∵∠B=60°,
∴△ABC、△ACD是等边三角形,
∴AB=BC=AC,∠CAD=60°,
∴AC=AD,
∵∠EAF=60°,
∴∠CAE=∠DAF,
∵∠ACE=∠D=60°,
∴△ACE≌△ADF,
∴AE=AF,
∴△EAF是等边三角形;
(2)四边形AECF的面积不变.
过点A作AG⊥BC于点G.
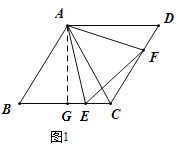
在Rt△ABG中,∠B=60°,
∴BG=![]() AB=3,
AB=3,
∴AG=![]() =
=![]() ,
,
∴S△ABC=S△ACD=![]() =
=![]() .
.
由(1)知△ACE≌△ADF,
∴S△ACE=S△ADF,
∴S四边形AECF=S△ACE+S△ACF= S△ADF+S△ACF=S△ACD=![]() ;
;
(3)∵S四边形AECF=S△AEF+S△ECF =![]() ,
,
∴S△AEF最小时S△ECF最大,
∵△AEF是等边三角形,
∴当AE⊥BC时S△AEF最小,
此时E是BC的中点,AE=![]() ,等边△AEF的EF边上的高为
,等边△AEF的EF边上的高为![]() =
=![]() ,
,
∴S△AEF=![]() =
=![]() ,
,
∴S△ECF= S四边形AECF - S△AEF =![]() =
=![]() ;
;
(4)将△ADN绕点A顺时针旋转120°得到△ABP,连接PM.
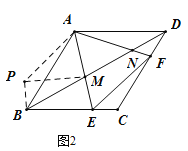
∵∠DAE=15°,∠EAF=60°,∠BAD=120°,
∴∠BAE=45°,∠BAP=∠DAF=15°,
∴∠MAN=∠MAP=60°,
∵AM=AM,AN=AP,
∴△MAN≌△MAP(SAS),
∴MN=PM,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ADN=![]() ∠ADC=30°,
∠ADC=30°,
∴∠AND=180°-15°-30°=135°,∠ANM=45°,
∴∠APB=∠AND=135°,∠APM=∠ANM=45°,
∴∠BPM=90°,
∴BP2+PM2=BM2,
∵BP=DN,PM=MN,
∴DN2+MN2=BM2.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.
的中点.
(1)如果点![]() 在线段
在线段![]() 上以
上以![]() 厘米
厘米![]() 秒的速度由
秒的速度由![]() 向
向![]() 点运动,同时点
点运动,同时点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动.
点运动.
①若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,
的运动速度相等,![]() 秒钟时,
秒钟时,![]() 与
与![]() 是否全等?请说明理由;
是否全等?请说明理由;
②点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() ?并说明理由;
?并说明理由;
(2)若点![]() 以②中的运动速度从点
以②中的运动速度从点![]() 出发,点
出发,点![]() 以原来运动速度从点
以原来运动速度从点![]() 同时出发,都逆时针沿
同时出发,都逆时针沿![]() 的三边运动,求多长时间点
的三边运动,求多长时间点![]() 与点
与点![]() 第一次在
第一次在![]() 的哪条边上相遇?
的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;
![]()
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户的养殖成本逐年增长,第一年的养殖成本为12万元,第3年的养殖成本为16万元.设养殖成本平均每年增长的百分率为x,则下面所列方程中正确的是( )
A. 12(1﹣x)2=16 B. 16(1﹣x)2=12 C. 16(1+x)2=12 D. 12(1+x)2=16
【答案】D
【解析】由题意可得:第二年的养殖成本为![]() ,
,
第三年的养殖成本为: ![]() ,
,
∴![]() .
.
故选D.
【题型】单选题
【结束】
8
【题目】一个布袋内只装有1个黑球和2个白球,这些球除颜色外其余都相同,随机摸出一个球后放回并搅匀,再随机摸出一个球,则两次摸出的球都是黑球的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在将式子![]() (m>0)化简时,
(m>0)化简时,
小明的方法是:![]() =
=![]() =
=![]() =
=![]() ;
;
小亮的方法是: ![]() ;
;
小丽的方法是:![]() .
.
则下列说法正确的是( )
A. 小明、小亮的方法正确,小丽的方法不正确
B. 小明、小丽的方法正确,小亮的方法不正确
C. 小明、小亮、小丽的方法都正确
D. 小明、小丽、小亮的方法都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△AOB中,A,B两点的坐标分别为(2,4)、(5,2).
(1)将△AOB向左平移3个单位长度,向下平移4个单位长度,得到对应的△A1O1B1,画出△A1O1B1并写出点A1、O1、B1的坐标.
(2)求出△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
【答案】(1)m的值为6;(2)17.
【解析】试题分析:
(1)由题意和根与系数的关系可得:x1+x2=2(m+1),x1x2=m2+5;由(x1-1)(x2-1)=28,可得:x1x2-(x1+x2)=27;从而得到:m2+5-2(m+1)=27,解方程求得m的值,再由“一元二次方程根的判别式”进行检验即可得到m的值;
(2)①当7为腰长时,则方程的两根中有一根为7,代入方程可解得m的值(此时m的取值需满足根的判别式△![]() ),将m的值代入原方程,可求得两根(此时两根和7需满足三角形三边之间的关系),从而可求得等腰三角形的周长;
),将m的值代入原方程,可求得两根(此时两根和7需满足三角形三边之间的关系),从而可求得等腰三角形的周长;
②当7为底边时,则方程的两根相等,由此可得“根的判别式△=0”,从而可得关于m的方程,解方程求得m的值,代入原方程可求得方程的两根,再由三角形三边之间的关系检验即可.
试题解析:
(1)(x1-1)(x2-1)=28,即x1x2-(x1+x2)=27,而x1+x2=2(m+1),x1x2=m2+5,
∴m2+5-2(m+1)=27,
解得m1=6,m2=-4,
又Δ=[-2(m+1)]2-4×1×(m2+5)≥0时,m≥2,
∴m的值为6;
(2) 若7为腰长,则方程x2-2(m+1)x+m2+5=0的一根为7,
即72-2×7×(m+1)+m2+5=0,
解得m1=10,m2=4,
当m=10时,方程x2-22x+105=0,根为x1=15,x2=7,不符合题意,舍去.
当m=4时,方程为x2-10x+21=0,根为x1=3,x2=7,此时周长为7+7+3=17
若7为底边,则方程x2-2(m+1)x+m2+5=0有两等根,
∴Δ=0,解得m=2,此时方程为x2-6x+9=0,根为x1=3,x2=3,3+3<7,不成立,
综上所述,三角形周长为17
点睛:(1)一元二次方程根与系数的关系成立的前提条件是方程要有实数根,即“根的判别式△![]() ”;(2)涉及三角形边长的问题中,解得的结果都需要用“三角形三边之间的关系”检验,看三条线段能否围成三角形.
”;(2)涉及三角形边长的问题中,解得的结果都需要用“三角形三边之间的关系”检验,看三条线段能否围成三角形.
【题型】解答题
【结束】
21
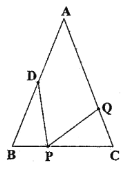
【题目】如图,已知在△ABC中,D是AB的中点,且∠ACD=∠B,若 AB=10,求AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com