
科目: 来源: 题型:
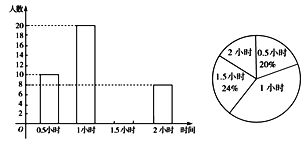
【题目】某中学为了解学生每天参加户外活动的情况,对部分学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)这次抽样调查,一共抽查了 名学生;
(2)补全频数分布直方图;
(3)若该中学共有1500名学生,请估计该校每天参加户外活动的时间为1小时的学生人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年“519(我要走)全国徒步日(江夏站)”暨第六届“环江夏”徒步大会5月19日在美丽的花山脚下降重举行.组委会(活动主办方)为了奖励活动中取得了好成绩的参赛选手,计划购买共100件的甲、乙两种纪念品发放.其中甲种纪念品每件售价120元,乙种纪念品每件售价80元.
(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各是多少件?
(2)设购买甲种纪念品![]() 件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
查看答案和解析>>
科目: 来源: 题型:
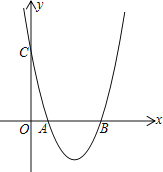
【题目】如图1,抛物线y=x2+bx+c与x轴交于A(1,0)、B(4,0),与y轴交于点C
(1) 求抛物线的解析式
(2) 抛物线上一点D,满足S△DAC=S△OAC,求点D的坐标
(3) 如图2,已知N(0,1),将抛物线在点A、B之间部分(含点A、B)沿x轴向上翻折,得到图T(虚线部分),点M为图象T的顶点.现将图象保持其顶点在直线MN上平移,得到的图象T1与线段BC至少有一个交点,求图象T1的顶点横坐标的取值范围
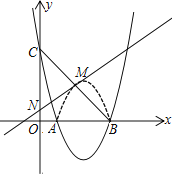
查看答案和解析>>
科目: 来源: 题型:
【题目】学校为了解学生对新闻、体育、动画、娱乐、戏曲类电视节目的喜爱情况,采用抽样的方法在七年级选取了一个班的同学,通过问卷调查,收集数据、整理数据,制作了如下两个整统计图,请根据下面两个不完整的统计图分析数据,回答以下问题:

(1)七年级的这个班共有学生_____人,图中![]() ______,
______,![]() ______,在扇形统计图中,“体育”类电视节目对应的圆心角为:______.
______,在扇形统计图中,“体育”类电视节目对应的圆心角为:______.
(2)补全条形统计图;
(3)根据抽样调查的结果,估算该校1750名学生中大约有多少人喜欢“娱乐”类电视节目?
查看答案和解析>>
科目: 来源: 题型:
【题目】某个体经营户了解到有一种盒装商品能畅销市场,就用4万元购进这种商品,面市后果然供不应求,他又用8.8万元购进了第二批这种商品,所购数量是第一批购进量的2倍,但每盒单价涨了4元,他在销售这种盒装商品时每盒定价都是56元,最后剩下的150盒按八折销售,很快售完,在这两笔生意中,这位个体经营户共赢利多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,B、D、E、F是直线 l上四点,在直线 l的同侧作△ABE和△CDF,且 AB∥CD,∠A=40°.作BG⊥AE于 G,FH⊥CD于 H,BG与 FH交于 P点.
(1)如图 1,B、E、D、F从左至右顺次排列,∠ABD=90°,求∠GPH;
(2)如图 2,B、E、D、F从左至右顺次排列,△ABE与△CDF均为锐角三角形,求∠GPH;
(3)如图 3,F、B、E、D从左至右顺次排列,△ABE为锐角三角形,△CDF为钝角三角形,则∠GPH的度 数为多少?请画出图形并直接写出结果,不需证明.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)求证:BD1=CE1;(2)当∠CPD1=2∠CAD1时,求CE1的长;
(3)连接PA,△PAB面积的最大值为 .(直接填写结果)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,第一象限内长方形ABCD,AB∥y轴,点A(1,1),点C(a,b),满足![]() +|b﹣3|=0.
+|b﹣3|=0.
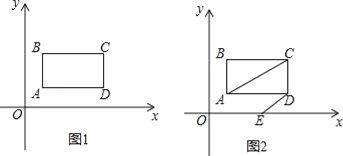
(1)求长方形ABCD的面积.
(2)如图2,长方形ABCD以每秒1个单位长度的速度向右平移,同时点E从原点O出发沿x轴以每秒2个单位长度的速度向右运动,设运动时间为t秒.
①当t=4时,直接写出三角形OAC的面积为 ;
②若AC∥ED,求t的值;
(3)在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An.
①若点A1的坐标为(3,1),则点A3的坐标为 ,点A2014的坐标为 ;
②若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com