
科目: 来源: 题型:
【题目】某市举办中学生“梦想杯”足球联赛,联赛记分办法是:胜1场得3分,平1场得1分,负1场得0分.复兴中学足球队参加了18场比赛,积24分.
(1)在这次足球联赛中,如果复兴中学足球队踢平场数与所负场数相同,那么它胜了几场?
(2)在这次足球联赛中,如果复兴中学足球队踢平场数多于所负场数,那么它的胜、平、负情况共有多少种?
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学组织学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车每日每辆租金为220元,60座客车每日每辆租金为300元.试问:
(1)春游学生共多少人,原计划租45座客车多少辆?
(2)若租用同一种车,要使每位同学都有座位,怎样租车更合算.
查看答案和解析>>
科目: 来源: 题型:
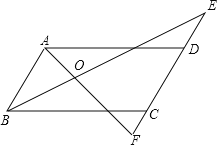
【题目】如图,BE平分∠ABC,∠ABC=2∠E,∠ADE+∠BCF=180°.
(1)请说明AB∥EF的理由;
(2)若AF平分∠BAD,判断AF与BE的位置关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学举行演讲比赛,七年级(1)班、(2)班根据初赛成绩各选出5名选手参加复赛,两个班所选出的5名选手的复赛成绩如下面条形统计图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差 | |
(1)班 | 85 | a | 85 | 70 |
(2)班 | 85 | 80 | b | c |
(1)根据条形统计图中的信息,求上表中a,b,c的值;
(2)请你分析说明哪个班级的复赛成绩较好.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.

查看答案和解析>>
科目: 来源: 题型:
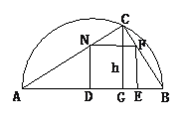
【题目】在直径为AB的半圆内,划出一块三角形区域,如图所示,使三角形的一边为AB,顶点C在半圆圆周上,其它两边分别为6和8,现要建造一个内接于△ABC的矩形水池DEFN,其中D、E在AB上,如图24-94的设计方案是使AC=8,BC=6.
(1)求△ABC的边AB上的高h.
(2)设DN=x,且![]() ,当x取何值时,水池DEFN的面积最大?
,当x取何值时,水池DEFN的面积最大?
(3)实际施工时,发现在AB上距B点1.85的M处有一棵大树,问:这棵大树是否位于最大矩形水池的边上?如果在,为了保护大树,请设计出另外的方案,使内接于满足条件的三角形中欲建的最大矩形水池能避开大树.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)先化简,再求值:(2-3x)(-3x-2)-5x(x-1)-(2x-1)2,其中x=-![]() ;
;
(2)已知xy2=-2,求xy(x2y5+3xy3-2y)的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】分解因式x2-4y2-2x+4y,细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式,过程为:x2-4y2-2x+4y=(x+2y)(x-2y)-2(x-2y)=(x-2y)(x+2y-2).这种分解因式的方法叫分组分解法,利用这种方法解决下列问题:
(1)分解因式:a2-4a-b2+4;
(2)若△ABC三边a、b、c满足a2-ab-ac+bc=0,试判断△ABC的形状.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com