
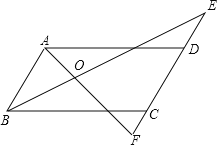
【题目】如图,BE平分∠ABC,∠ABC=2∠E,∠ADE+∠BCF=180°.
(1)请说明AB∥EF的理由;
(2)若AF平分∠BAD,判断AF与BE的位置关系,并说明理由.
【答案】(1)见解析;(2)AF⊥BE,见解析.
【解析】
(1)结论:AB∥EF,只要证明∠E=∠ABE 即可;
(2)根据平行线的性质以及角平分线的定义即可证明.
(1)证明:∵BE平分∠ABC,
∴∠ABE=![]() ∠ABC.
∠ABC.
又∵∠ABC=2∠E,
即∠E=![]() ∠ABC,
∠ABC,
∴∠E=∠ABE.
∴AB∥EF;
(2)解:结论:AF⊥BE.
理由:∵∠ADE+∠ADF=180°,
∠ADE+∠BCF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;
∴∠DAB+∠CBA=180°,
∵∠OAB=![]() DAB,∠OBA=
DAB,∠OBA=![]() ∠CBA,
∠CBA,
∴∠OAB+∠OBA=90°,
∴∠AOB=90°,
∴AF⊥BE.
故答案为:(1)见解析;(2)AF⊥BE,见解析.


科目:初中数学 来源: 题型:
【题目】(1)计算:(-8xy2)(-![]() x)3+(-2x4)4+2x10(-2x2)3
x)3+(-2x4)4+2x10(-2x2)3
(2)先化简,再求值:(y+2)(y2-2y+1)-y(y2+1),其中y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
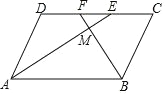
【题目】如图,在 ABCD 中,AE、BF 分别平分∠DAB 和∠ABC,交 CD 于点 E、F,AE、BF 相交于点 M.
(1)求证:AE⊥BF;
(2)判断线段 DF 与 CE 的大小关系,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.
性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等.
理解:如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.
应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O.
(1)求证:△AOB和△AOE是“友好三角形”;
(2)连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.
探究:在△ABC中,∠A=30°,AB=4,点D在线段AB上,连接CD,△ACD和△BCD是“友好三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的![]() ,请直接写出△ABC的面积.
,请直接写出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:(2-3x)(-3x-2)-5x(x-1)-(2x-1)2,其中x=-![]() ;
;
(2)已知xy2=-2,求xy(x2y5+3xy3-2y)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①表示的是某综合商场今年1~5月的商品各月销售总额的情况,图②表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图①、图②,解答下列问题:
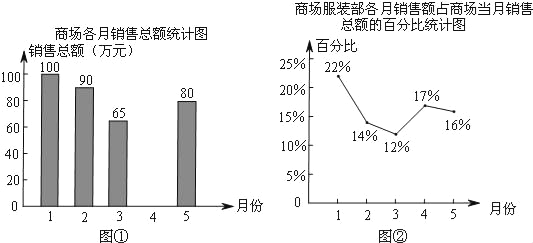
(1)来自商场财务部的数据报告表明,商场1~5月的商品销售总额一共是410万元,请你根据这一信息将图①中的统计图补充完整;
(2)商场服装部5月份的销售额是多少万元?
(3)小刚观察图②后认为,5月份商场服装部的销售额比4月份减少了.你同意他的看法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全国爱眼日是每年的6月6日,2013年世界爱眼日主题确定为“关爱青少年眼健康”,某中学为了解该校学生的视力情况,采用抽样调查的方式,从视力正常、轻度近视、中度近视、重度近视四个方面调查了若干名学生的视力情况,并根据调查结果制作了如下两幅统计图。


根据图中提供的信息解答下列问题:
(1)一共随机调查了多少人?
(2)补全人数统计图;
(3)若该校共有1500名学生,请你估计该校学生视力正常的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】火车匀速通过隧道时,火车在隧道内的长度![]() (米)与火车行驶时间
(米)与火车行驶时间![]() (秒)之间的关系用图象描述如图所示,有下列结论:
(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确的结论是_____.(把你认为正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
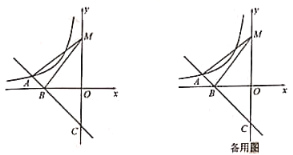
【题目】如图,平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 在第二象限内的图像相交于点A,与
在第二象限内的图像相交于点A,与![]() 轴的负半轴交于点B,与
轴的负半轴交于点B,与![]() 轴的负半轴交于点C.
轴的负半轴交于点C.
(1)求∠BCO的度数;
(2)若![]() 轴上一点M的纵坐标是4,且B点坐标为(-3,0),求AM的长.
轴上一点M的纵坐标是4,且B点坐标为(-3,0),求AM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com