
科目: 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连结BD.求证:
(1)△BAD≌△CAE;
(2)BD⊥CE

查看答案和解析>>
科目: 来源: 题型:
【题目】(阅读理解)
在解方程组或求代数式的值时,可以用整体代入或整体求值的方法,化难为易.
(1)解方程组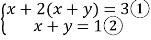
(2)已知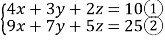 ,求x+y+z的值
,求x+y+z的值
解:(1)把②代入①得:x+2×1=3.解得:x=1.
把x=1代入②得:y=0.
所以方程组的解为![]() ,
,
(2)①×2得:8x+6y+4z=20.③
②﹣③得:x+y+z=5.
(类比迁移)
(1)若![]() ,则x+2y+3z= .
,则x+2y+3z= .
(2)解方程组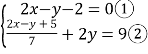
(实际应用)
打折前,买39件A商品,21件B商品用了1080元.打折后,买52件A商品,28件B商品用了1152元,比不打折少花了多少钱?
查看答案和解析>>
科目: 来源: 题型:
【题目】自2020年开始,新冠病毒疫情严峻,某爱心组织紧急筹集了部分资金,计划购买甲、乙两种救灾物品共4000件送往武汉,已知每件甲种物品的价格比每件乙种物品的价格贵10元,用450元购买甲种物品的件数恰好与用400元购买乙种物品的件数相同.
(1)求甲、乙两种救灾物品每件的价格分别是多少元?
(2)经调查,灾区对乙种物品件数需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这4000件物品,需筹集资金多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的积.
(1)请你用列表或画树状图的方法,求摸出的这两个数的积为6的概率;
(2)小敏和小颖做游戏,她们约定:若这两个数的积为奇数,小敏赢;否则,小颖赢.你认为该游戏公平吗?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D, 其图象与x轴的交点A、B的横坐标分别为﹣1,3.与y轴负半轴交于点C,当a=![]() 时,△ABD是_______三角形;要使△ACB为等腰三角形,则a值为______
时,△ABD是_______三角形;要使△ACB为等腰三角形,则a值为______
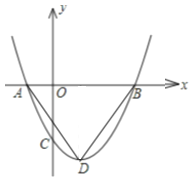
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于_______海里.

查看答案和解析>>
科目: 来源: 题型:
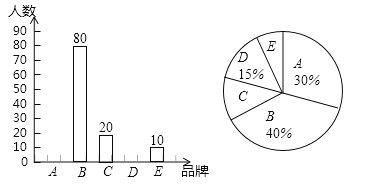
【题目】“共享单车,绿色出行”,现如今骑共享单车出行不但成为一种时尚,也称为共享经济的一种新形态,某校九(1)班同学在街头随机调查了一些骑共享单车出行的市民,并将他们对各种品牌单车的选择情况绘制成如下两个不完整的统计图(A:摩拜单车;B:ofo单车;C:HelloBike).请根据图中提供的信息,解答下列问题:
(1)求出本次参与调查的市民人数;
(2)将上面的条形图补充完整;
(3)若某区有10000名市民骑共享单车出行,根据调查数据估计该区有多少名市民选择骑摩托单车出行?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数y=![]() (k≠0)的图象过点C,则该反比例函数的表达式为_______.
(k≠0)的图象过点C,则该反比例函数的表达式为_______.

查看答案和解析>>
科目: 来源: 题型:
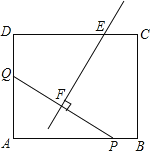
【题目】如图,在矩形ABCD中,AB=12,AD=10.点Q从点D出发沿DA以每秒1个单位长度的速度向点A匀速运动;点P从点A出发沿AB以每秒2个单位长度的速度向点B匀速运动.伴随P、Q的运动,直线EF保持垂直平分PQ于点F,交射线DC于点E,点P、Q同时出发,当点P到达B点时停止运动,点Q也随之停止.设点P运动时间为t秒(0<t<6),t=____________时,EF能平分矩形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com