
科目: 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=﹣x+5的图象与反比例函数![]() (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.

(1)求反比例函数的解析式及点B坐标;
(2)在第一象限内,当一次函数y=-x+5的值大于反比例函数![]() (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )

A.AB=DC,AD=BCB.AB∥DC,AD∥BC
C.AB∥DC,AD=BCD.OA=OC,OB=OD
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)观察思考:如图,线段AB上有两个点C、D,请分别写出以点A、B、C、D为端点的线段,并计算图中共有多少条线段;
(2)模型构建:如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性;
(3)拓展应用:8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行多少场比赛?
请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】国庆节放假时,小华一家三口一起乘小轿车去乡下探望爷爷、奶奶和外公、外婆.早上从家里出发,向东走了4千米到超市买东西,然后又向东走了3千米到爷爷家,中午从爷爷家出发向西走了12千米到外公家,晚上返回家里.
![]()
(1)若以家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来;
(2)若小轿车每千米耗油0.09升,求小明一家从出发到返回家所经历路程小车的耗油量.(精确到0.1升)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,有一块矩形铁皮,长110cm,宽70cm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖的方盒,如果要制作的无盖的方盒的底面积为4500cm2,那么铁皮各角应切去的正方形边长是多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两名同学做摸球游戏,他们把四个分别标有1,2,3,4的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)若从袋中随机摸出一球,则摸出的球的标号恰好是偶数的概率是 ;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,∠ACB=2∠B,(1)如图①,当∠C=90°,AD为∠ABC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.请证明AB=AC+CD;
(2)①如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请直接写出你的结论,不要求证明;
②如图③,当∠C≠90°,AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明.
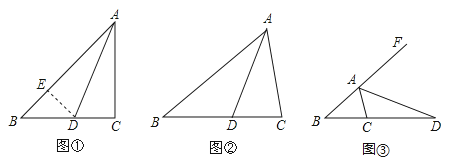
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务.
在初中数学课本中重点介绍了提公因式法和运用公式法两种因式分解的方法,其中运用公式法即运用平方差公式:a2-b2=(a+b)(a-b)和完全平方公式:a2±2ab+b2=(a±b)2进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式ax2+bx+c(a≠0)变形为a(x+m)2+n的形式,我们把这样的变形方法叫做多项式ax2+bx+c的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:x2+8x+7
=x2+8x+16-16+7
=(x+4)2-9
=(x+4+3)(x+4-3)
=(x+7)(x+1)
根据以上材料,完成相应的任务:
(1)利用“多项式的配方法”将x2+2x-3化成a(x+m)2+n的形式为_______;
(2)请你利用上述方法因式分解:
①x2+6x+8;
②x2-6x-7.
查看答案和解析>>
科目: 来源: 题型:
【题目】计算
(1)(﹣7)﹣(+5)+(﹣4)﹣(﹣10);
(2)![]() .
.
(3)(﹣24)×(1+![]() ﹣
﹣![]() );
);
(4)36÷(﹣3)2×(![]() ﹣1)+(﹣1)3+(﹣1)2.
﹣1)+(﹣1)3+(﹣1)2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com