
科目: 来源: 题型:
【题目】如图所示,有若干边长为1的正方形卡片,第1次并排摆2张黑色卡片,铺成一个长方形;第2次在黑色卡片上方和右侧摆白色卡片,所有卡片铺成了一个较大的长方形;第3次继续在白色卡片上方和右侧摆黑色卡片,所有卡片铺成了一个更大的长方形;以此类推,请解决以下问题:
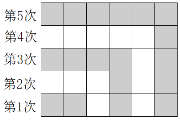
(1)仅第10次要用去______张卡片,摆完第10次后,总共用去_______张卡片.
(2)你知道 2+4+6+8+……+2n的结果是多少吗?写出结果,结合图形规律说明你的理由.
(3)求出从第51次至第100次所摆卡片的数量之和.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平行四边形ABCD中,点E为BC边上一点,AE和BD交于点F,已知△ABF的面积等于 6,△BEF的面积等于4,则四边形CDFE的面积等于___________

查看答案和解析>>
科目: 来源: 题型:
【题目】一天早晨,乐乐以80米/分的速度上学,5分钟后乐乐的爸爸发现他忘了带数学书,爸爸立即骑自行车以280米/分的速度去追乐乐,并且在途中追上了他,请解决以下问题:
(1)爸爸追上乐乐用了多长时间?
(2)爸爸追上乐乐后,乐乐搭爸爸的自行车回到学校,结果提前了10分钟到校,若爸爸搭上乐乐后的骑行速度为240米/分,求乐乐家离学校有多远.
查看答案和解析>>
科目: 来源: 题型:
【题目】彩虹服装店用![]() 元购进
元购进![]() 件衬衣,很快全部售完.服装店老板以每件
件衬衣,很快全部售完.服装店老板以每件![]() 元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:
元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:元).他卖完这
(单位:元).他卖完这![]() 件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学从学生入学开始就积极开展环保教育,半学期后随机对部分学生的环保习惯养成情况进行了问卷调查,问卷中的环保习惯有:①随手关灯;②充电后及时拔充电器插头;③生活用水合理重复利用;④不用或少用一次性餐具;⑤少用塑料袋多用环保袋;⑥绿色出行,同学勾选出自己已经养成的环保习惯,学校将结果绘成了如图所示的不完整的条形统计图和扇形统计图.
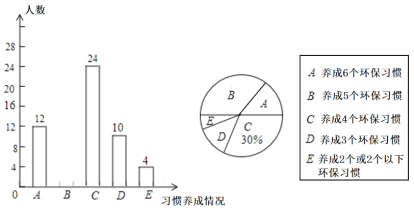
(1)求在这次调查中,一共抽查了多少名学生?
(2)通过计算补全条形统计图.
(3)已知全校共有学生1200人,请估计全校所有学生中已经养成3个或3个以上环保习惯的同学共有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2011个小正方形,则需要操作的次数是( )
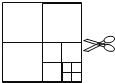
A. 669 B. 670 C. 671 D. 672
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;

(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
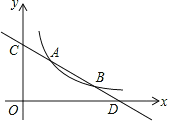
【题目】直线y=kx+b与反比例函数y=![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】【阅读学习】 刘老师提出这样一个问题:已知α为锐角,且tanα=![]() ,求sin2α的值.
,求sin2α的值.
小娟是这样解决的:
如图1,在⊙O中,AB是直径,点C在⊙O上,∠BAC=α,所以∠ACB=90°,tanα=![]() =
=![]() .
.
易得∠BOC=2α.设BC=x,则AC=3x,则AB=![]() x.作CD⊥AB于D,求出CD= (用含x的式子表示),可求得sin2α=
x.作CD⊥AB于D,求出CD= (用含x的式子表示),可求得sin2α=![]() = .
= .
【问题解决】
已知,如图2,点M、N、P为圆O上的三点,且∠P=β,tanβ =![]() ,求sin2β的值.
,求sin2β的值.


查看答案和解析>>
科目: 来源: 题型:
【题目】计算:
(1)23×(-5)-(-3)÷![]() ;
;
(2)(-3)×![]() +8×(-2
+8×(-2![]() )-11÷(-
)-11÷(-![]() );
);
(3)(-1)2-(-1![]() )×(-24);
)×(-24);
(4)![]() (-2)2-(
(-2)2-(![]() )3+[1+(-
)3+[1+(-![]() )2×(-1
)2×(-1![]() )].
)].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com