
科目: 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.观察下面的点阵图和相应的等式,探究其中的规律:
(1)下图反映了任何一个三角形数是如何得到的,认真观察,并在④后面的横线上写出相应的等式;
![]()

(2)通过猜想,写出(1)中与第八个点阵相对应的等式 ;
(3)从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.结合(1)观察下列点阵图,并在⑤看面的横线上写出相应的等式.


(4)通过猜想,写出(3)中与第n个点阵相对应的等式 ;
(5)判断256是不是正方形数,如果不是,说明理由;如果是,256可以看作哪两个相邻的“三角形数”之和?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 中,
中,![]() ,点
,点![]() 是斜边
是斜边![]() 上的中点,过点
上的中点,过点![]() 作
作![]() 边上的垂线
边上的垂线![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .
.
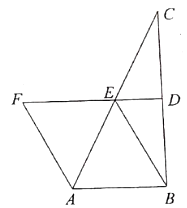
(1)找出图中与![]() 相等的所有线段.
相等的所有线段.
(2)若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )

A. 24m B. 25m C. 28m D. 30m
查看答案和解析>>
科目: 来源: 题型:
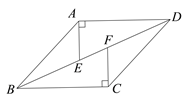
【题目】如图,在菱形ABCD中,AE⊥AD交BD于点E,CF⊥BC交BD于点F.
(1)证明:△ADE≌△CBF;
(2)连接AF、CE,四边形AECF是菱形吗?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
﹣4,﹣|﹣![]() |,0,
|,0,![]() ,﹣3.14,2019,﹣(+5),+1.88,
,﹣3.14,2019,﹣(+5),+1.88,
(1)正数集合:{ _____…};(2)负数集合:{__________…};
(3)分数集合:{_______…};(4)非负整数集合:{_______…}.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 三边长分别为
三边长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积,小明同学在求面积时先画了一个每个小正方形的边长均为1的正方形网格,再在网格中画出格点
,求这个三角形的面积,小明同学在求面积时先画了一个每个小正方形的边长均为1的正方形网格,再在网格中画出格点![]() (
(![]() 各个顶点都在网格的格点上).如图1所示,这样借用网格(不需
各个顶点都在网格的格点上).如图1所示,这样借用网格(不需![]() 的高)就能算出三角形的面积,这种方法叫构造法.
的高)就能算出三角形的面积,这种方法叫构造法.
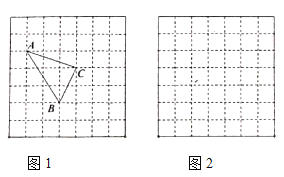
(1)![]() 的面积为___________________.
的面积为___________________.
(2)若![]() 的三边长分别为
的三边长分别为![]() 、
、![]() 、
、![]() ,请在图2的网格中画出
,请在图2的网格中画出![]() ,使得
,使得![]() 的三个顶点都在格点上,求此三角形的面积.
的三个顶点都在格点上,求此三角形的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙二人用4张扑克牌(分别是红桃2,红桃3,黑桃4,方片5)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先取一张,取出的牌不放回,乙从剩余的牌中取一张.
(1)设![]() 、
、![]() 分别表示甲、乙取出的牌面上的数字,写出
分别表示甲、乙取出的牌面上的数字,写出![]() 的所有结果;
的所有结果;
(2)若甲取到红桃3,则乙取出的牌面数字比3大的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
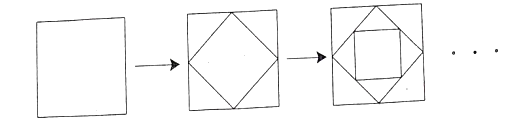
【题目】如图,依次连接边长为1的小正方形各边的中点,得到第二个小正方形,再依次连接第二个小正方形各边的中点得到第三个小正方形,按这样的规律第2019个小正方形的面积为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别交两轴于点
分别交两轴于点![]() ,点
,点![]() 的横坐标为4,点
的横坐标为4,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析式;
的解析式;
(3)在平面内是否存在这样的点![]() ,使以
,使以![]() 为顶点的四边形为平行四边形?若存在,请求出点
为顶点的四边形为平行四边形?若存在,请求出点![]() 的坐标;若不存在,不必说明理由.
的坐标;若不存在,不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com