
科目: 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
利用数形结合思想回答下列问题:
(1)数轴上表示1和3两点之间的距离 .数轴上表示-12和-6的两点之间的距离是 .
(2)数轴上表示x和-4的两点之间的距离表示为 .
(3)|x-2|+|x+4|的最小值为 时,能使|x-2|+|x+4|取最小值的所有整数x的和是 .
(4)若数轴上两点A、B对应的数分别是-1、3,现在点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动,当点A与点B之间的距离为3个单位长度时,求点A所对应的数是多少?
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,![]() 点P从点A出发,沿折线AB-BC向终点C运动,在AB上以每秒8个单位长度的速度运动,在BC上以每秒2个单位长度的速度运动.动点Q从点C出发,沿CA方向以每秒
点P从点A出发,沿折线AB-BC向终点C运动,在AB上以每秒8个单位长度的速度运动,在BC上以每秒2个单位长度的速度运动.动点Q从点C出发,沿CA方向以每秒![]() 个单位长度的速度运动.P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P的运动时间为t秒.
个单位长度的速度运动.P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P的运动时间为t秒.
(1)用含t的代数式表示线段AQ的长.
(2)当点P在线段AB上运动时,求PQ与△ABC一边垂直时t的值.
(3)设△APQ的面积为S(S>0),求S与t的函数关系式.
(4)当△APQ是以PQ为腰的等腰三角形时,直接写出t的值.

查看答案和解析>>
科目: 来源: 题型:
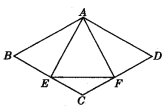
【题目】已知:如图所示,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
(1)试说明:AE=AF;
(2)若∠B=60°,点E,F分别为BC和CD的中点,试说明:△AEF为等边三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y1=k1x+2与反比例函数y2=![]() 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
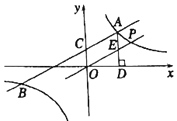
(1)k1= ,k2= ;
(2)根据函数图象可知,当y1>y2时,x的取值范围是 ;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求直线OP的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在等边△ABC中取点P,使得PA,PB,PC的长分别为3,4,5,将线段AP以点A为旋转中心顺时针旋转60°得到线段AD,连接BD,下列结论:
①△ABD可以由△APC绕点A顺时针旋转60°得到;②点P与点D的距离为3;③∠APB=150°;
④S△APC+S△APB=![]() ,其中正确的结论有( )
,其中正确的结论有( )
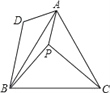
A. ①②④B. ①③④C. ①②③D. ②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】读句画图并完成计算:如图,直线AB与直线CD交于点C ,

(1)过点P作PQ∥CD,交AB于点Q;
(2)过P作PR⊥CD于点R;
(3)若∠DCB=150,求∠PQC的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=6,AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )
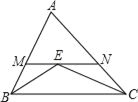
A. 12B. 10C. 8D. 不确定
查看答案和解析>>
科目: 来源: 题型:
【题目】为了丰富课外活动,某校将购买一些乒乓球拍和乒乓球,某商场销售一种乒乓球拍和乒乓球,乒乓球拍每副定价80元,乒乓球每盒定价20元,“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一副乒乓球拍送一盒乒乓球;
方案二:乒乓球拍和乒乓球都按定价的90%付款.
某校要到该商场购买乒乓球拍20副,乒乓球![]() 盒(
盒(![]() >20且为整数).
>20且为整数).
(1)若按方案一购买,需付款 元(用含![]() 的整式表示,要化简); 若按方案二购买,需付款 元(用含
的整式表示,要化简); 若按方案二购买,需付款 元(用含![]() 的整式表示,要化简).
的整式表示,要化简).
(2)若![]() 30,通过计算说明此时按哪种方案购买较为合算?
30,通过计算说明此时按哪种方案购买较为合算?
(3)当![]() 30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读并解决其后的问题:我们将四个有理数![]() 、
、![]() 、
、![]() 、
、![]() 写成
写成![]()
![]() 的形式,称它为由有理数
的形式,称它为由有理数![]() 、
、![]() 、
、![]() 、
、![]() 组成的二阶矩阵,称
组成的二阶矩阵,称![]() 、
、![]() 、
、![]() 、
、![]() 为构成这个矩阵的元素,如由有理数
为构成这个矩阵的元素,如由有理数![]() 、2、3、
、2、3、![]() 组成的二阶矩阵是
组成的二阶矩阵是![]()
![]() ,
,![]() 、2、3、
、2、3、![]() 是这个矩阵的元素,当且仅当两个矩阵相同位置上的元素相等时,我们称这两个二阶矩阵相等,下面是两个二阶矩阵的加法运算过程:①
是这个矩阵的元素,当且仅当两个矩阵相同位置上的元素相等时,我们称这两个二阶矩阵相等,下面是两个二阶矩阵的加法运算过程:①![]()
![]() +
+![]()
![]() =
=![]()
![]() =
=![]()
![]() ,②
,②![]()
![]() +
+![]()
![]() =
=![]()
![]() =
=![]()
![]() ,
,
(1)通过观察上述例子中矩阵加法运算的规律,可归纳得二阶矩阵的加法运算法则是:两个二阶矩阵相加, .
(2)①计算:![]()
![]() +
+![]()
![]() ;
;
②若![]()
![]() +
+![]()
![]() =
=![]()
![]() ,求
,求![]() 的值;
的值;
(3)若记A=![]()
![]() ,B=
,B=![]()
![]() ,试依据二阶矩阵的加法法则说明A+B=B+A成立
,试依据二阶矩阵的加法法则说明A+B=B+A成立
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com