（1）点A表示的有理数是　 　，点B表示的有理数是　 　，点C表示的有理数是　 　．

（2）当点P运动到点B时，点Q从点O出发，以每秒6个单位长度的速度沿数轴在点O和点C之间往复运动．

①求t为何值时，点Q第一次与点P重合？

②当点P运动到点C时，点Q的运动停止，求此时点Q一共运动了多少个单位长度，并求出此时点Q在数轴上所表示的有理数．

(1)方法1，已知标杆DE＝2.2 m，求该塔的高度；

(2)方法2，测量得∠ACB＝47.5°，已知tan47.5°≈1.09，求该塔的高度；

(3)假如该塔的高度在方法1和方法2测得的结果之间，你认为该塔的高度大约是多少米？

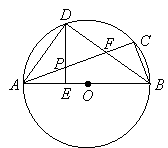
【1】求证：∠DAC ＝∠DBA；

【2】求证：是线段AF的中点

【3】若⊙O 的半径为5，AF ＝ ，求tan∠ABF的值．

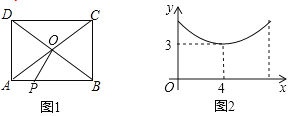
【题目】如图1，在长方形中，对角线与交于点O，动点P从点A出发，沿匀速运动，到达点B时停止，设点P所走的路程为x．线段的长为y，若y与x之间的函数图象如图2所示，图象与y轴的交点为E．则E的纵坐标为_______________，则长方形的周长为____________．

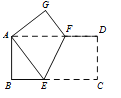
A. AF＝AE B. △ABE≌△AGF C. EF＝ D. AF＝EF

（1）在图1中作线段BC的中点P；

（2）在图2中，在OB、OC上分别取点E、F，使EF∥BC．

A. 北偏西30° B. 南偏西30° C. 南偏东60° D. 南偏西60°

一般地，把（a≠0）记作a，记作“a 的圈c次方”.

(1)直接写出计算结果：2③= ，(-3)④ = ，⑤= .

(2)计算 24÷23 + (-8)×2③.

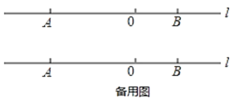
（1）OA=_______cm，OB=________cm；

（2）若点 C 是线段AB的中点，求线段 CO 的长；

（3）若动点 P、Q分别从 A、B同时出发，向右运动，点P的速度为2 厘米/秒，点Q的速度为1厘米/秒，设运动时间为x秒，当 x=_____秒时，PQ=4cm；

（4）有两条射线 OC、OD 均从射线 OA 同时绕点O顺时针方向旋转，OC旋转的速度为6度/秒，OD 旋转的速度为2度/秒.当OC与OD第一次重合时，OC、OD 同时停止旋转，设旋转时间为 t 秒，当t为何值时，射线OC⊥OD

①该产品90天内日销售量（m件）与时间（第x天）满足一次函数关系，部分数据如下表：

②该产品90天内每天的销售价格与时间（第x天）的关系如下表：

（1）求m关于x的一次函数表达式；

（2）设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品哪天的销售利润最大？最大利润是多少？【提示：每天销售利润=日销售量×（每件销售价格-每件成本）】

（3）在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果．