
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
查看答案和解析>>
科目: 来源: 题型:
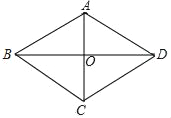
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠BAO=∠DAO.
(1)求证:平行四边形ABCD是菱形;
(2)请添加一个条件使菱形ABCD为正方形.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是 ( )
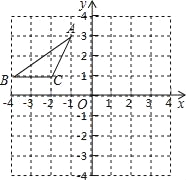
A. A1(4,4),C1(3,2) B. A1(3,3),C1(2,1) C. A1(4,3),C1(2,3) D. A1(3,4),C1(2,2)
查看答案和解析>>
科目: 来源: 题型:
【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目: 来源: 题型:
【题目】先化简,再求值.
(1)6a2-5a(a+2b-1)+a(-a+10b)+5,其中a=-1,b=2008;
(2)3xy2﹣[xy﹣2(2xy﹣![]() x2y)+2xy2]+3x2y,其中x、y满足(x+2)2+|y﹣1|=0.
x2y)+2xy2]+3x2y,其中x、y满足(x+2)2+|y﹣1|=0.
查看答案和解析>>
科目: 来源: 题型:
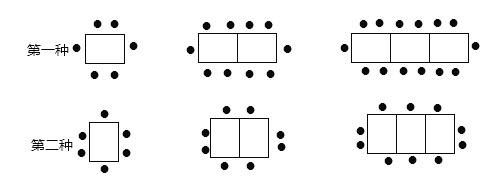
【题目】(9分)某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)有4张桌子,用第一种摆设方式,可以坐___________人;当有![]() 张桌子时,用第二种摆设方式可以坐___________人(用含有n的代数式表示).
张桌子时,用第二种摆设方式可以坐___________人(用含有n的代数式表示).
(2)一天中午,餐厅要接待85位顾客共同就餐,但餐厅中只有20张这样的长方形桌子可用,且每4张拼成一张大桌子,若你是这家餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?
查看答案和解析>>
科目: 来源: 题型:
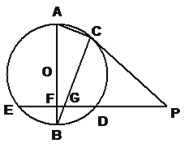
【题目】已知,AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直于AB于点F,交BC于点G,∠A=∠BCP.
(1)求证:PC是⊙O的切线;
(2)若点C在劣弧AD上运动,其条件不变,问应再具备什么条件可使结论BG2=BF·BO成立,(要求画出示意图并说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com