
科目: 来源: 题型:
【题目】在一元二次方程中,有著名的韦达定理:对于一元二次方程ax2+bx+c=0(a≠0),如果方程有两个实数根x1,x2,那么x1+x2=﹣![]() ,x1x2=
,x1x2=![]() (说明:定理成立的条件△≥0).比如方程2x2﹣3x﹣1=0中,△=17,所以该方程有两个不等的实数解.记方程的两根为x1,x2,那么x1+x2=
(说明:定理成立的条件△≥0).比如方程2x2﹣3x﹣1=0中,△=17,所以该方程有两个不等的实数解.记方程的两根为x1,x2,那么x1+x2=![]() ,x1x2=﹣
,x1x2=﹣![]() ,请根据阅读材料解答下列各题:
,请根据阅读材料解答下列各题:
(1)已知方程x2﹣3x﹣2=0的两根为x1、x2,且x1>x2,求下列各式的值:
①x12+x22;②![]() ;
;
(2)已知x1,x2是一元二次方程4kx2﹣4kx+k+1=0的两个实数根.
①是否存在实数k,使(2x1﹣x2)(x1﹣2x2)=﹣![]() 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由.
②求使![]() 的值为整数的实数k的整数值.
的值为整数的实数k的整数值.
查看答案和解析>>
科目: 来源: 题型:
【题目】把下列各数分别填入相应的集合里
-4, ![]() ,
, ![]() , 0, -3.14, 717, -(+5) +1.88,
, 0, -3.14, 717, -(+5) +1.88, ![]()
(1)正有理数集合:{_____________________________…}
(2)负数集合:{_____________________________…}
(3)整数集合:{_____________________________ …}
(4)分数集合:{______________________________…}
查看答案和解析>>
科目: 来源: 题型:
【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)求收工时,检修小组在![]() 地的何方向?距离
地的何方向?距离![]() 地多远?
地多远?
(2)在第几次纪录时距![]() 地最远?
地最远?
(3)若汽车行驶每千米耗油0.4升,问从![]() 地出发,检修结束后再回到
地出发,检修结束后再回到![]() 地共耗油多少升?
地共耗油多少升?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,
①若△ABC是以BC为斜边的直角三角形,求k的值.
②若△ABC是等腰三角形,求k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某班同学为了解2019年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行整理如下:
月均用水量x(t) | 频数(户) | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
| 2 | 0.04 |

请解答下列问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB∥CD,点E在直线AB上,点G在直线CD上,点P在直线AB.CD之间,∠AEP=40°,∠EPG=900
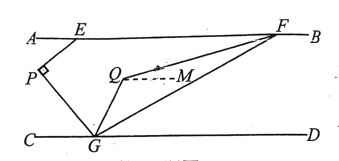
(1)填空:∠PGC=_________0;
(2)如图, 点F在直线AB上,联结FG,∠EFG的平分线与∠PGD的平分线相交于点Q,当点F在点E的右侧时,如果∠EFG=30°,求∠FQG的度数;
解:过点Q作QM∥CD
因为∠PGC+∠PGD=1800
由(1)得∠PGC=_______0,
所以∠PGD=1800-∠PGC=________0,
因为GQ平分∠PGD,
所以∠PGQ=∠QGD=![]() ∠PGD=_________0
∠PGD=_________0
(下面请补充完整求∠FQG度数的解题过程)
(3)点F在直线AB上,联结FG,∠EFG的平分线与∠PGD的平分线相交于点Q.如果∠FQG=2∠BFG,请直接写出∠EFG的度数.
查看答案和解析>>
科目: 来源: 题型:
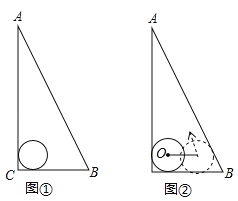
【题目】如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
(1)如图①,当圆形纸片与两直角边AC、BC都相切时,试用直尺与圆规作出射线CO;(不写作法与证明,保留作图痕迹)
(2)如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,求圆心O运动的路径长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2﹣2x+c(a≠0)与x轴、y轴分别交于点A,B,C三点,已知点A(﹣2,0),点C(0,﹣8),点D是抛物线的顶点.
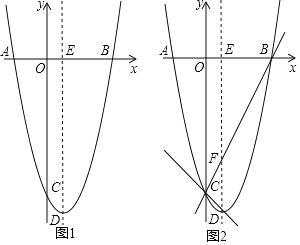
(1)求抛物线的解析式及顶点D的坐标;
(2)如图1,抛物线的对称轴与x轴交于点E,第四象限的抛物线上有一点P,将△EBP沿直线EP折叠,使点B的对应点B'落在抛物线的对称轴上,求点P的坐标;
(3)如图2,设BC交抛物线的对称轴于点F,作直线CD,点M是直线CD上的动点,点N是平面内一点,当以点B,F,M,N为顶点的四边形是菱形时,请直接写出点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题情境
小明和小丽共同探究一道数学题:
如图①,在△ABC中,点D是边BC的中点,∠BAD=65°,∠DAC=50°,AD=2,
求AC.
探索发现
小明的思路是:延长AD至点E,使DE=AD,构造全等三角形.
小丽的思路是:过点C作CE∥AB,交AD的延长线于点E,构造全等三角形.
选择小明、小丽其中一人的方法解决问题情境中的问题.
类比应用
如图②,在四边形ABCD中,对角线AC、BD相交于点O,点O是BD的中点,
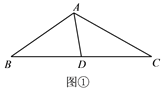
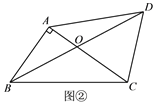
AB⊥AC.若∠CAD=45°,∠ADC=67.5°,AO=2,则BC的长为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com