
����Ŀ����һԪ���η����У���������Τ�ﶨ��������һԪ���η���ax2+bx+c��0��a��0�����������������ʵ����x1��x2����ôx1+x2����![]() ��x1x2��
��x1x2��![]() ��˵����������������������0�������緽��2x2��3x��1��0�У�����17�����Ը÷������������ȵ�ʵ���⣮�Ƿ��̵�����Ϊx1��x2����ôx1+x2��
��˵����������������������0�������緽��2x2��3x��1��0�У�����17�����Ը÷������������ȵ�ʵ���⣮�Ƿ��̵�����Ϊx1��x2����ôx1+x2��![]() ��x1x2����
��x1x2����![]() ��������Ķ����Ͻ�����и��⣺
��������Ķ����Ͻ�����и��⣺
��1����֪����x2��3x��2��0������Ϊx1��x2����x1��x2�������и�ʽ��ֵ��
��x12+x22����![]() ��
��
��2����֪x1��x2��һԪ���η���4kx2��4kx+k+1��0������ʵ������
���Ƿ����ʵ��k��ʹ��2x1��x2����x1��2x2������![]() �����������ڣ����k��ֵ���������ڣ���˵�����ɣ�
�����������ڣ����k��ֵ���������ڣ���˵�����ɣ�
����ʹ![]() ��ֵΪ������ʵ��k������ֵ��
��ֵΪ������ʵ��k������ֵ��
���𰸡�(1) ��x12+x22��13, ��![]() ;(2) �ٲ�����,���ɼ���������k����2��3��5
;(2) �ٲ�����,���ɼ���������k����2��3��5
��������
��1����Τ�ﶨ��д��x1+x2��x1x2��ֵ���ѣ�x1+x2��2������ȫƽ����ʽ������â٣�ͨ����ֵ��âڣ�
��2�����������0ʱ��k��ȡֵ��Χ����Τ�ﶨ��д����k��ʾx1+x2��x1x2��ֵ����ֱ�Ӱѵ�ʽ���չ�����Σ�����x1+x2��x1x2��ʽ�ӣ������k���ڻ���ʽ�ӵõ�k�ڷ�ĸ�ķ�ʽ������ʽ�ӵ�ֵΪ������k��ȡֵ��Χȷ��k��ֵ��
��1����x2��3x��2��0��b2��4ac������3��2��4������2����17��0��
��x1+x2��3��x1x2����2��
��x12+x22����x1+x2��2��2x1x2��32��2������2����9+4��13��
��![]() ��
��
��2���߷���������ʵ������
��b2��4ac������4k��2��44k��k+1����0��
��k��0��x1+x2��1��x1x2��![]() ��
��
�١ߣ�2x1��x2����x1��2x2����2x12��5x1x2+2x22��2��x12+2x1x2+x22����9x1x2��2��x1+x2��2��9x1x2��
��![]() ��
��
��ã�k��![]() ����k��0ì�ܣ�
����k��0ì�ܣ�
�����k��ֵ��ʹ��2x1��x2����x1��2x2������![]() ������
������
��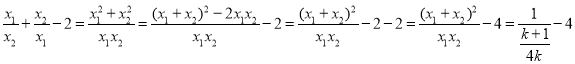
![]() ��
��
��![]() ��ֵΪ������
��ֵΪ������
��k+1����1����2����4��
�֡�k��0��
��k����2��3��5.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ͬһƽ���ڣ�![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() �����ӳ�����һ�㣨ͼ�����нǾ�ָС��
�����ӳ�����һ�㣨ͼ�����нǾ�ָС��![]() �Ľǣ�.���н��ۣ���
�Ľǣ�.���н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() .������.ȷ.���۵ĸ����У� ��.
.������.ȷ.���۵ĸ����У� ��.
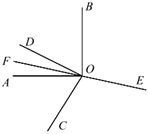
A.4��B.3��C.2��D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
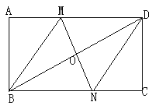
����Ŀ����ͼ���ھ���ABCD�У��Խ���BD�Ĵ�ֱƽ����MN��AD�ཻ�ڵ�N������BM��DN.
��1����֤���ı���BMDN�����Σ�
��2����AB=4��AD=8����MD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڡ�ABC��,��D.E�ֱ��ڱ�AB,AC��,DE��BC,������Ҫ��ͼ�����
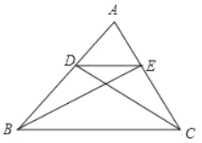
(1)����E��ֱ��BC�Ĵ��߽�ֱ��BC�ڵ�F;
(2)��D��ֱ��______�ľ�������߶�EF�ij���
(3)����BE.CD,EBC�����______DBC�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ͬѧΪ�˽�2019��ijС����ͥ�¾���ˮ�������������˸�С�����ּ�ͥ�������������ݽ����������£�
�¾���ˮ��x��t�� | Ƶ�������� | Ƶ�� |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
| 2 | 0.04 |

�����������⣺
��1���������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������
��2�����С����ˮ��������15t�ļ�ͥռ�������ͥ�����İٷֱȣ�
��3������С����1000����ͥ�����ݵ������ݹ��ƣ���С���¾���ˮ������20t�ļ�ͥ��Լ�ж��ٻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ħ����������������ع�900��ħ�������߲μӣ����δ������ֽ���3��3��ħ��������ί�������������ƽ���ֵ�30������ÿ������30��ͬʱ���б��������ʱ��С��8��İ����߽�����һ�ֽ�����ͼ��3��3��ħ����A����30�����������ʱ��ͳ��ͼ��
��1����գ�A����3��3��ħ�������߽�����һ�ֽ������______�ˣ�
��2����գ���A����30�����������ʱ��Ϊ9���������7��������3����
��a=______��b=______��
�����ʱ���ƽ������______�룬��λ����______�룬������______�룮
��3����3��3��ħ��������������������һ�£������A�����ͳ�ƽ��������3��3��ħ�����������һ�ֽ����Լ�ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ϣ�С������������һ�����֡��������ݳ����Ҫ��ѡ�����Σ����ѹ����ĵ��������л�������塢���غ���λѡ��û�й�������.
��1����������һ���ĸ���;
��2�����С��������һ�µ�һ������ô������һ���˲�����һ����ȴû���еĸ����Ƕ��٣�����������״ͼ�������б����ȷ���д���������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ִ�С��ͬ����������κ�һ��ȱ�ǵij�����ƴ�ɳ����� ABCD�����У�NH=NG 1cm ���� BF acm ��
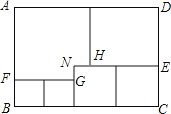
��1���ú� a �Ĵ���ʽ�ֱ��ʾ CE��DE��
��2������ ABCD ���ܳ������ú� a �Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����㣺
�Ķ����и�ʽ��![]() ��
��![]() ��
��![]() ����
����
�ش������������⣺
��1����֤����5��0.2��10=__________��510��0.210=__________��
��2��ͨ��������֤�����ɵó���![]() =__________��
=__________��![]() =__________��
=__________��
��3����Ӧ���������ʼ��㣺
��![]()
��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com